在《哈利波特》系列电影中有一个场景,要想到达伦敦国王十字车站9¾站台,必须要通过一道屏障墙。这种魔法在量子力学中是存在的,但需要注意的是,对于像身体这样的宏观物体,穿过墙壁的可能性极低。当物体越来越小时,这种概率显著上升,以至于缩小到亚原子粒子时,这种隧穿效应会一直发生。
量子隧穿
想象一下,有一个网球在一个无摩擦的盒子中来回滚动。当球撞击到盒子的侧边时,它就会弹回。让球脱离盒子的方法是,使球有足够的能量跳过盒子的侧板或者将盒子侧板撞破。如果这不是网球而是一个电子,那么情况可能就不一样了。
量子力学的其中一个规则是,量子物体具有波粒二象性。这意味着电子可以表现得像波一样,严格来说是一种概率波。那么它在空间中的位置由波函数定义,它只能告诉我们在特定位置找到它的概率。虽然你认为电子可能在盒子里,但它的波函数使它在盒子外的概率非零,因此电子也可能出现在盒子外。
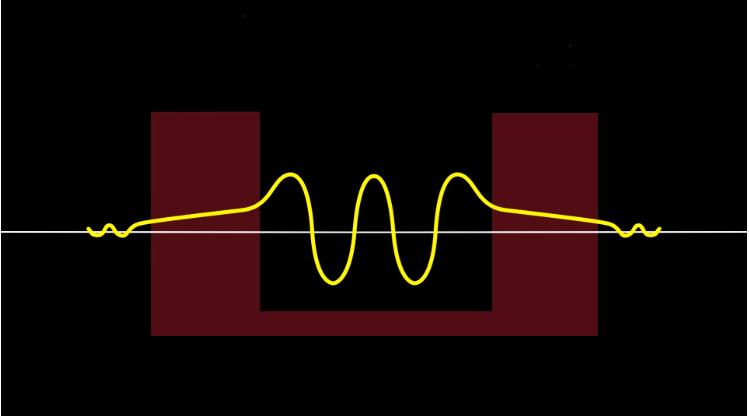
事实上,量子力学表明,粒子的波函数存在于整个空间中,存在于整个宇宙直至无穷大。所以量子力学的惊人启示是,当你认为电子在这个盒子里时,它在火星上的概率不为零。这个概率非常小,但重要的是这个概率是非零的。那么,是什么支配了这种行为呢?我们可以将其归因于海森堡不确定性原理。基本上,这个原理表明,粒子位置的不确定性乘以动量的不确定性必须大于一个有限的数,这意味着我们无法100%确定地知道该电子的位置。
波函数方程
使用薛定谔方程可以找到电子的波函数,它使我们有可能在任何位置找到它。因此,让我们仔细研究一下,弄清楚它如何向我们展示在盒子外找到电子的可能性。
薛定谔方程是由埃尔温·薛定谔在1926年左右提出的,它是描述物质波动性质的方程。方程中的希腊字母ψ是波函数,尽管波函数取决于时间和位置,但我们只看它如何随位置变化,以了解电子在势垒周围的行为。波函数可以是正的也可以是负的,但它的平方总是正的。碰巧的是,波函数的平方是位置x的函数,它给出了在该位置找到粒子的概率。
薛定谔方程左边的第一部分是作用于波函数的动能算子,第二部分是作用于波函数的势能算子。在等号的右边,它是作用在波函数上的总能量。薛定谔方程基本上是能量守恒的陈述:动能加上势能等于总能量。但我们不仅有能量,还有作用于粒子波函数的能量算子。
现在,我们可以求解这个盒子里粒子的波函数。它可以分为三个部分,盒子内、壁板内和盒子外,如下图。事实上,盒子外的波函数与盒子内的相同,只不过振幅小得多。前面讲过,波函数的平方代表了找到粒子的概率,只要盒子外的波函数非零,我们就可以在盒子外找到电子的存在。
不能穿墙
那么,为什么这种数学形式并不适用于大型物体?例如,我们为什么不能穿墙呢?如果你仔细查看Ⅱ区中的波函数,你会发现它取决于几个因素:势垒的厚度、势垒的高度以及粒子的质量。对于像人类这样的宏观物体,我们的质量是如此之大,障碍物的厚度如此之大,以至于波函数将具有极小的值,从而使概率变得极小。
事实上,如果你粗略地计算一下手或身体穿过墙的概率,这个结果大约是10^-40量级。尽管这在物理上并非不可能,但在统计上是不可能的。
原文链接:https://www.toutiao.com/i7070738658512421384
本站文章部分来自于互联网,已注明出处。 未注明原文出处皆为原创文章,转载同样请注明出处并添加链接。
猜你喜欢
发表评论
电子邮件地址不会被公开。 必填项已用*标注