在刘慈欣传奇般的《三体》中,三体文明可谓受尽了折磨,无数文明世代的更替,无休无止的脱水冲泡,相信每一个三体人都有一种生不如死的感觉,这一切都是由于他们的三颗恒星带来的三体问题,其实不止是三体文明,就连我们生活在天堂一般的太阳系的地球人也对三体问题很头疼,那么到底什么才是三体问题呢?
一.都是月亮惹的祸
话说牛顿出版《自然哲学的数学原理》后,顿生“天上地下,唯我独尊”之感,仰视星空不禁大笑:“我笑那第谷无谋,开普勒少智,行星运动规律居然耗尽一生光阴,且看我小人家再加上月亮。”言毕奋笔疾书,良久喟然长叹:“真JB难。”
这就是三体问题的起源,开普勒的行星运动三大定律考虑的是太阳和行星之间只有引力作用情况下的规律,别看各大行星都算了一遍,其实行星之间的引力都忽略了,说白了就是两个质点在只有引力作用下的运动轨迹,只要懂万有引力定律和微积分确实是唾手可得,可爵爷加上月亮之后就不一样了,他得考虑太阳地球月亮之间的相互引力了,爵爷确实没有解出来,因为这就变成了三个质点在只有引力作用下的运动问题了,这就变成了三体问题了,不过爵爷说的没有那么粗俗,他说的是“除非研究月球,我的头从来没有疼过”,这句话可以理解为爵爷的倨傲,也反映了爵爷的无奈。
为什么月球让爵爷这么头疼呢?因为爵爷的计算结果和天文观测不一致。
咱们还是先来回顾一下开普勒行星运动第一定律,第一定律是说行星围绕太阳运转的轨道是一个椭圆形,太阳就位于这个椭圆的一个焦点上,这样一来就有了近日点和远日点,对于各大行星包括地球来说,近日点和远日点的出现和公转周期相同,行星每绕太阳一圈就会出现一次近日点和远日点,这是很好理解的,可是到了月亮上问题就出来了。
月球绕地球的轨道也是一个椭圆形,地球就位于月球椭圆轨道的一个焦点,月球也就有了近地点和远地点,所谓的超级月亮就是月球位于近地点的“十五的月亮”,可是超级月亮并不是年年有呀,这是由于月球的近地点和远地点并不是年年有的,对于行星来说,其它星球的引力影响都可以忽略不计,就是一个简单的二体问题,而对于月球来说,太阳的引力是不能忽略不计的,这就成了一个三体问题。
按照牛顿的计算,月球近地点每17.8年出现一次,就是每17.8年出现一次超级月亮,而早在古希腊时期,人们就知道了超级月亮每8.85年出现一次,这都差了一倍了,已经不能用计算误差来解释了。
当然天文观测是不可能出错的,既然和天文观测不一致,那就可能是理论错了,这就是万有引力理论的第一次危机。
牛顿当然不会承认自己错的,不过他也没有提出解决办法,这也有情可原,毕竟他太忙了呀,除了物理和数学的这点业余爱好,他还有神学和炼金术要研究,除了这些研究工作,还得和胡克莱布尼茨撕逼,除了这俩不省心的主儿,他还得管着大英帝国的金融,都是费心的事情呀。
爵爷不认为万有引力定律有错并不代表别人不这么认为,法国数学家克莱罗就认为万有引力定律有问题,需要修正一下。
二、万有引力定律的危机
这个克莱罗是个名副其实的天才,比牛顿还天才,18岁上就凭借对空间曲线的研究成为了法兰西科学院最年轻的院士,牛顿在这个岁数上也不过是刚刚跨进剑桥大学的校门。
牛顿去世二十年后的1747年,克莱罗宣称引力的大小与距离的平方成反比的定律(就是万有引力定律)并不能解决月球近地点的问题,他提出了要对万有引力定律加以修正,在原来万有引力定律上加一个立方反比项。
此言一出,立刻引起了轩然大波,不过也得到了一些人的支持,这就包括欧拉,欧拉也认为万有引力定律需要修正,但是有一个问题一定要注意到,那就是增加修正项后可以解决月球的问题,那么是不是会影响别的星星呢,欧拉随后发现,增加修正项后,月球的问题解决了,可是对于离太阳更近的水星来说问题就更大了,更加不符合观测了,这说明这条路是一条死路。
克莱罗也很快意识到了自己的错误,两年后他收回了论文,改进了计算方法,在牛顿力学的框架下解决了月球近地点问题,随后数学家达朗贝尔也宣称解决了这个问题,可欧拉却百思不得其解,他问克莱罗怎么做的,克莱罗却没有理他,这可难不倒欧拉,他向圣彼得堡科学院建议,把月球问题作为学院奖的题目并报以丰厚的奖金,有钱不挣王八蛋,何况这又是克莱罗已经解决的问题,克莱罗毫无争议地获得了奖金,不过论文也到了学院奖评委之一的欧拉手中,欧拉恍然大悟,也修正了自己的计算,三人都得到了一致的结果。
牛顿得到的地球绕太阳周期和月球近地点进动周期之比是3/4m,m=0.0748他们三人得出的结论是周期之比是3/4m+225/32m^2,他们三人结果比爵爷的结果多了一个m的平方,牛顿的结果对应的是太阳引力扰动的的一阶效应,而三人增加的平方项对应的二阶效应。
有点糊涂,是吧?那就说人话。首先是太阳影响了地月系统引起了月球近地点的进动,这就是牛顿考虑的一阶效应,但是这种进动反过来又影响了太阳和月亮的相对位置变化的方式,从而改变了引力扰动的强度,这就是二阶效应,明白了吧,再来看看欧拉克莱罗达朗贝尔计算的结果。
他们仨计算的月球近地点进动周期是10.5年,这还是不对呀,不是古希腊人说是8.55年嘛,不要着急嘛,既然有了二阶效应那就有三阶四阶五阶……效应,只要计算下去,肯定能和观察一致的,不过计算起来太麻烦了,都是大数学家,指明方向就可以了,剩下的就让凡人去算吧。
这段历史生动地诠释了什么叫“你大爷就是你大爷”,估计欧拉又想起了师爷莱布尼茨被牛顿揍得如丧家之犬老师约翰.伯努利被羞得无地自容的时候了,一人灭三代估计也只有牛顿爵爷能做得出来了。
大获全胜的是牛顿,可占便宜最大的还是欧拉,欧拉虽然没有得到圣彼得堡学院的奖金,他也得不到因为他根本就不会,可是他得钱也不少,估计还要超过克莱罗,并不是他贪污了奖金,大数学家干不出这事来,他得到了另外一份奖金,这份奖金来自英国政府,奖金高达2万英镑,这笔钱太多了,牛顿一辈子也没有挣这么多钱,当时最著名的科学奖项科普利奖也不过才100英镑。
到底是什么事情值得英国政府这么下血本呢?这就是海上霸权。
大英帝国称雄天下靠的就是海上霸权,可航海最重要的是什么?当然是方向。可怎么确定方向呢?晚上看北极星白天看太阳,没错,不过那是初级阶段,要想在茫茫大海上部迷失,还得知道自己的位置,这靠看北极星和太阳就不行了,因为北极星和太阳确定只是纬度,要想知道自己的位置还得知道经度,怎么知道经度呢?当然是要看时间,我们都知道地球自转一圈是24小时,只要知道了当地时间再和出发时的时间一对比就大体知道经度了,可是问题知道时间呀,那就要看月亮了。
这就是月距法,月球在星河之中穿行,通过测量月球和特定恒星的角度就可以知道时间,这样的话出发之前测一测时间,在海上再测一次就知道了时间差,知道了时间差就知道了经度差就知道了自己的位置,不过这有一个前提就是要提前知道月球的位置,这就需要一张月表,而且要误差极小。
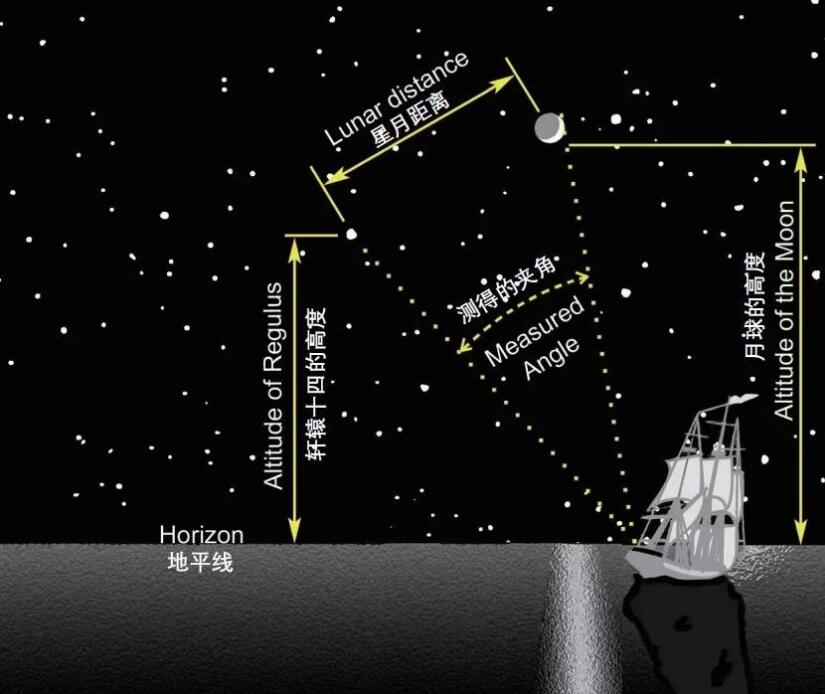
当初大英帝国海军部还为这个事情请教过牛顿爵爷,这也是爵爷头疼的原因,后来英国皇家天文官用欧拉的公式计算出来了精确的月表,因此欧拉也拿到了300英镑,看起来欧拉有点亏,才拿了1.5%,其实一点也不亏,因为最后这笔奖金最后被一个钟表匠拿走了,一群科学家都白折腾了。
当然没有白折腾,欧拉从对月球问题的探索中得出了三体问题的新思路,这就是限制性三体问题。
三、限制性三体问题
限制性三体问题是说三个质点中有两个大质量的,它们相互作用,还有一个小质点,两个大质量的质点可以对小质点有作用力,但是小质点对大质点的作用可以忽略不计,其实这就是简化的日地月系统。
摆脱了月球的限制,欧拉的聪明才智顿时爆发了,对于限制性三体问题,他得出来了三个特解。
在欧拉特解中,三个质点都围绕质心做椭圆运动且永远在一条直线上。
欧拉特解的提出,是三体问题的一个极大推动,不过欧拉并没有得出所有特解,下面就到了拉格朗日的表演时间。
拉格朗日同样是天才,这都不用多说了,要想干这活,不是天才都干不了。他18岁上就创立了微积分的变分法,同年成为教授,又是一个比牛顿还牛的天才,第二年在欧拉的推荐下,成为了普鲁士科学院的通讯院士。
让他一举成名的就是三体问题,他找到了欧拉没有找到的限制性三体问题的另外两个解。
拉格朗日找到的另外两个解位于等边三角形的顶点,就是说三个质点将永远保持一个等边三角形,这两个解有点过于奇葩了,拉格朗日认为这只是一个数学解,不大可能在星空中观测到,可是宇宙就是这样神奇,在100多年后,天文学家发现木星和在木星轨道上的希腊小行星群和特洛伊小行星群还有太阳恰好构成一个等边三角形。
限制性三体问题的这五个特解统称为拉格朗日点。
这五个点就是拉格朗日点,其中L1L2L3是欧拉解出来的,L4L5是拉格朗日解出来的,在拉格朗日点天体受到的引力是平衡的,这次刚刚升空詹姆斯韦伯太空望远镜的目的地就是L2,距离地球大约150万公里。
限制性三体问题的巅峰就是发现了海王星。法国天文学家勒维耶发现天王星和水星的轨道和开普勒轨道不完全相符,因此预测天王星附近应该还有一颗行星,这就是海王星,他觉得水星附近也应该还有一颗,这次是真没有,至于水星轨道的问题是由广义相对论解决的。
四、生日庆典
说起生日会想起什么?蛋糕、蜡烛、许愿?对,还有长寿面,还有呢?生日礼物,这肯定是不可缺少的,什么?还有甲午战争,那是慈禧老佛爷的,一看您就是一位忧国忧民的仁人志士,可是你能想到数学题吗?你能想到谁的生日礼物是一道数学题吗?而且收到礼物的寿星公还欢天喜地的,这寿星公莫非有病吧。
这寿星公一切健康而且还是一位国王,他就是挪威和瑞典国王奥斯卡二世,这位国王数学学得不错,还创办了一份数学杂志,恰逢他六十大寿,杂志的主编就打算出一道数学题邀请数学家们来解题为国王贺寿。
奥斯卡二世闻听,龙颜大悦,立刻准奏,事后证明这是国王最明智的一个举动,后世历史学家知道他都是由于这道数学题。
既然国王交办的差事,当然不能怠慢,主编请来了自己的老师魏尔斯特拉斯作为评委,这位老师就是写出极限定义的那位大师,微积分在他的手上才站稳了脚跟。
可出什么题呢?这就是N体问题。
具有任意多个质点的系统,其中任何两点间的作用力满足牛顿定律,在任意两个点不发生碰撞的情况下,试给出每个点的坐标,这个坐标可以以时间的某个已知函数作为变量的级数表示,并且对于所有的取值,该级数是一致收敛的。
并且设立了丰厚的奖金,大约2500瑞典克朗,这就是奥斯卡国王奖,投稿方式为匿名,截止日期为1888年6月1日,不过考虑到这个题有点难,就算没人做出来也不要紧。
即使在这次竞赛结束时这个问题还没有被解决,奖金仍然将颁发给完整地阐述和解决了力学其他问题的研究者。
这才叫帝王气势,根本就不在乎那点小钱。
这顿时引来了无数英雄,倒不是差那点钱,主要是为了扬名立万,当然有钱赚就更好了。
比赛截止日时,共受到了12篇论文,却有16封信,这是由于要求是匿名投稿,投稿人需要寄出两封信,其中一封是论文,另外一封里面写作者的姓名和联系方式,要求作者在信封上写上同一句话来证明是两封信都是自己写的,评委只能看到论文而不能看到作者姓名,为什么是16封而不是24封,因为只有四个人留下了真实姓名,其它的还真匿名了。
当魏尔斯特拉斯打开一封写着“繁星无法超越”的论文时,他惊呆了,他认为这篇论文完美地解决了三体问题,获奖是当之无愧的。
1889年1月20日,在国王生日的前夜,奥斯卡二世在斯德哥尔摩主持了颁奖仪式,这才打开了和论文一起寄来的作者信息,这篇论文的作者就是庞加莱。
五、繁星无法超越
庞加莱号称最后一位数学和物理的全才,往前看,他是牛顿之后数学和天体力学的一座丰碑,往后看,他在爱因斯坦前得出了狭义相对论,再往后看,他的数学思想是广义相对论的基础,要不是在数学里陷的太深,估计就没有爱因斯坦什么事了。
在家世上,也就比小王子德布罗意差点,那真没办法,谁叫德布罗意家族是世袭王侯呀,不过要比贵公子普朗克要强一点,贵公子家是诗书传家,他们家是政治豪门,一个堂哥是法国总统,一个堂哥是教育部长。
家世上虽然略有差别,有一点还是相同的,就是他们都是自己家族的最高荣耀,这就是“尔曹身与名俱灭,不废江河万古流”。
庞加莱从小就有“神童”美誉,读书过目不忘,中学时就被称为“数学巨人”,面对如此天才,大学时学校当局诚惶诚恐,唯恐天妒英才,专门给他安排了一场测试,一是测试一下他的天才程度,另外就是担心他心理出问题,别像当年伽罗瓦一样早逝。
这样的天赋,当然无论干什么都是第一,从小到大不管什么竞赛他都抢着参加,反正第一都是他的,可是在他26岁时参加的一次比赛他居然输了,是可忍孰不可忍?这时候奥斯卡奖来了,庞加莱决定无论如何也要把奥斯卡收入囊中。
庞加莱开始以为这没有多难,大佬们已经指明了方向,沿着路走下去就行了,可是两年之后他发现错了,以为大佬们用的是微扰法,是忽略小质点的,要想解决三体问题,必须要用新方法,可新方法在哪呢?结论是没有,毕竟欧拉拉格朗日都想不到的方法哪还有啊。
那没有怎么办?造一个出来呗,于是微分方程定性理论就诞生了。
对于微分方程定性理论,庞加莱非常满意,他得意地说:“这一问题将为未来几代的数学家提供取之不竭的成果来源,如此多的工作需要去完成,即使是向前迈几步,也会占用我的余生。现在至少我懂得,没有人能够独立地解决这个问题。我们这代人不可能完全理解它。”
现在庞加莱已经胜券在握,1887年5月17日,他寄出了自己的论文,在信封上写下了那句著名的“繁星无法超越”。
接下来就是激动人心的时刻了。
庞加莱获奖的消息第二条就登上了欧洲各大报纸的头条,整个欧洲都沸腾了,法国政府立刻授予了庞加莱法国荣誉军团勋章,庞加莱一跃成为了民族英雄。
可是日中则昃,俗话说就是乐极生悲,庞加莱说什么也没有想到,他写的那句“繁星无法超越”简直就是一句谶语。
按照程序,杂志下一期就要刊登庞加莱的论文,在校对过程中,编辑有些问题难以理解,于是要庞加莱解释一下,庞加莱在解释过程中发现自己错了。
这可是天大的事情,说好听点,这叫一时疏忽,说难听了呢,这就是学术造假了。庞加莱立刻写信要求停止论文印刷,可是已经晚了,论文已经印刷了一部分了,当务之急就是立刻收回所有预印本并销毁,预印本倒是都是都收回来了,可是并没有销毁。
更大的问题是已经有流言传出来了,说是论文有错误,这让魏尔斯特拉斯非常气愤,毕竟他也为庞加莱站台了,现在摆在庞加莱面前的有两条路,一条就是承认错误,名声受损,一条就是隐瞒错误,等别人发现错误,那就更丢人了。
可庞加莱不走寻常路,他决定两条路都不走,他要走第三条道路。第三条道路就是自己修正论文中的错误,重新得出正确结论。
一年后,庞加莱终于修正了论文中的错误,重新出版了论文,不过这次他要自费了,他支付了3585克朗,想想奖金才2500克朗,这下庞加莱都赔到姥姥家去了,不过无所谓了,对于数学家来说,只要不丢人不丢到姥姥家就行。
痛定思痛之后,庞加莱决定他的理论编撰成书,赔了那么多,总得找补一下,这就是《天体力学新方法》,就是这本书确定了庞加莱成为牛顿之后数学和天体力学丰碑的地位。
那么庞加莱到底错在哪了呢?他又发现了什么呢?
六、混沌蝴蝶
纽约的一只蝴蝶扇扇翅膀就会引起华盛顿的一场风暴,这就是蝴蝶效应,这是由美国气象学家洛伦兹在1963年提出的,此后风起云涌,混沌学就此诞生。
但是混沌学就肇始于庞加莱。
在庞加莱获得奥斯卡奖的论文初稿中,庞加莱认为三个三体要么趋向于平衡,要么趋向于周期或者准周期运动,总而言之就是三体系统会是一个稳定系统。
在修稿过程中,庞加莱证明了一个结果,相交的不变曲线极有可能不稳定,不稳定的曲线和稳定曲线一旦出现一次相交就会接连不断地多次相交,这些相交曲线会形成网状构,并不断穿越网眼,形成更加纷乱复杂的网眼,整个系统最终将陷入混乱无序中,这就是混沌。
庞加莱不只是认识到了混沌,还窥探到了产生混沌的天机,他认为初始行为很规范的系统,在受到扰动之后,或者参数、初始条件出现微小变化之后,在后续演化中,可能引起复杂的、甚至根本上的变化,系统可能不再稳定,而是出现不可预测的混乱。
这就是蝴蝶效应产生的原因。
蝴蝶扇动翅膀只是对天气系统产生了一个微小的扰动,可是在后续演化中就引起了复杂的变化,这个变化就造成了系统的不稳定,出现不可预测的混乱,这就有可能造成华盛顿的一场风暴。
所以说长期天气预报是不可能的,就算是蝴蝶不扇动翅膀,某个人也可能打个喷嚏,这个喷嚏就可能引发一场龙卷风。
对于N体问题,人们也发现了很多很多美丽的特解。
在《三体》中,魏成还发现了更多多姿多彩的特解,可是这样照样拯救不了三体文明,可能一颗流星滑过或者遥远的地方爆发了一颗超新星都有可能对系统造成扰动,从而走向不可知的混沌。
原文链接:https://www.toutiao.com/i7047669605669585441
本站文章部分来自于互联网,已注明出处。 未注明原文出处皆为原创文章,转载同样请注明出处并添加链接。
猜你喜欢
发表评论
电子邮件地址不会被公开。 必填项已用*标注



