根据颗粒空间理论,物理学概念上最短的距离是普朗克长度,量子力学认为物质小到这个幅度上就不可分割了,因此普朗克长度也被认为是宇宙最小长度单位,它指的是光子在一个普朗克时间中走过的距离,大致为1.6×10-33cm。
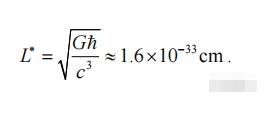
普朗克长度
由此可见,空间是均匀的,各向同性的。如果我们在宇宙的某个体积内将一些大小为300Mpc的区域分开,(1Mpc=1000000pc=3260000光年。1pc约等于3.26光年,)并计算每个星系的数量,那么所有区域的大小几乎都是相同的。在星团和超级星团的情况下也会得到同样的结果。一个大小为300Mpc的体积,从星系的空间分布近似均匀开始,被称为宇宙中的均匀性单位。然而,在最近的区域,在哈勃观测到的体积中,物质的分布根本就不均匀。相反,星系在大小约为1mpc分布不均匀。

利用传统的宇宙膨胀理论,我们可以提出这样一个问题:在这种条件下,一个规则的膨胀速度如何对应于速度-距离比例定律υ=H·R。根据弗里德曼理论,该定律只在物质在空间中的均匀分布时才有效。星系的散布看起来好像一个宇宙哲学论。
这就是自哈勃常数诞生以来一直存在的悖论。1999年,发现者艾伦·桑德奇写道:“这仍然是个谜团。”
2019年9月,德国科学家利用引力透镜效应计算出哈勃常数为82.4,从而推算得到宇宙年龄为114亿岁,比主流观点认为的137亿岁年轻20多亿岁。
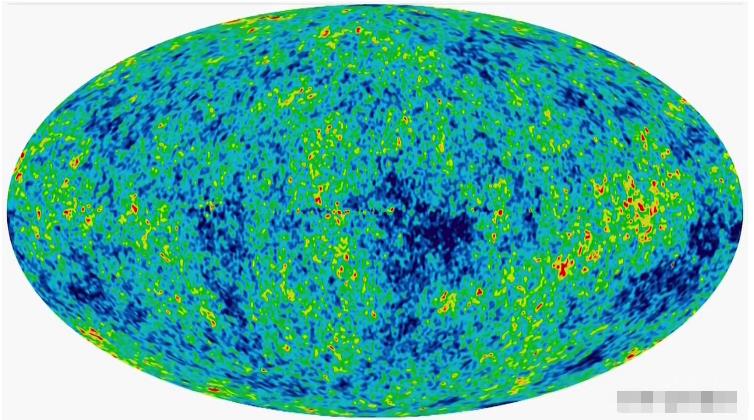
欧洲航天局于2013年3月21日宣布,根据普朗克卫星的测量结果得出新的哈勃常数值为67.80±0.77(km/s)/Mpc
1974~1976年,桑德奇和塔曼又用七种距离指标的方法重新修订哈勃常数,得H=55,只及哈勃当年测定值的1/10。
颗粒空间理论的一个基本结论是,v2/c2是指空间单元的相对变形,而加速度a是这种变形的变化率。

重力势能描述的是边界一个球的半径Rφball=const2·R2,而不是φstar=const1/R,完全模拟多普勒效应和恒星在边界上的辐射导致中心观察者观测到的红移:
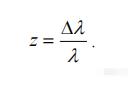
当速度超过50,000km/s时,应使用以下公式:
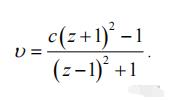
这个修正并没有改变我们对物理上的基本结论,当υ/c<1,多普勒效应依旧
因此,应该重申,宇宙中既没有膨胀,也没有加速膨胀,也没有暗能量。
哈勃定律在星系的散布分布中,距离只有几个Mpc的情况依旧正确。
大约40年前,发现基本单位的变形在宇宙中占主导地位:径向形和螺旋形。正是由于变形,我们可以确定物质的分布是否均匀和各向同性。

这一事实揭示了桑德奇的谜团:即使我们考虑的距离不是1.5Mpc,而是缩小1000倍,忽略了恒星的速度,哈勃定律将实现,因为它是由我们想象的球R表面的重力势(逃逸速度)决定的。
让我们考虑一下下面的例子。据了解,一个局部星系群的质量为1.5×1012太阳质量,到观测者R≈的距离为1.5Mpc。这种情况这一组的逃逸速度
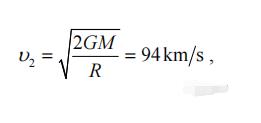
根据哈勃定律

可以看出,哈勃常数只表明了空间的结构,而不是宇宙的膨胀。H的这个值与实验结果完全一致。
这个常数表明,它的平均值既不依赖于朝向星系的方向,也不依赖于星系的距离。这种稳定性的原因是显而易见的:它描述了宇宙空间单位的均匀和各向同性变形。
原文链接:https://www.toutiao.com/article/7098305628489155106
本站文章部分来自于互联网,已注明出处。 未注明原文出处皆为原创文章,转载同样请注明出处并添加链接。
猜你喜欢
发表评论
电子邮件地址不会被公开。 必填项已用*标注