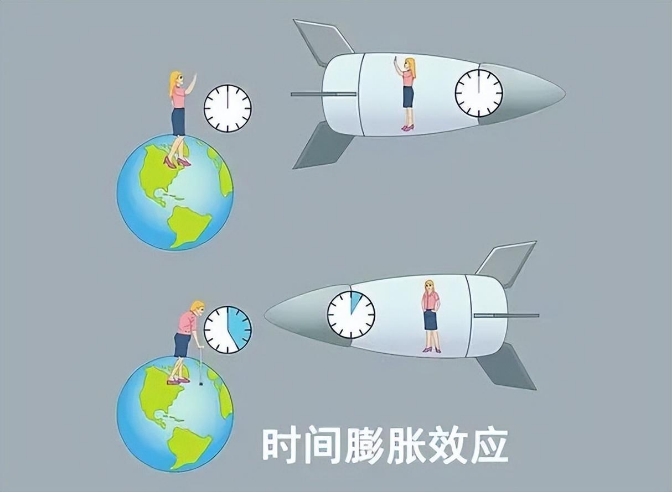
爱因斯坦的相对论已经提出了一百多年了,但是直到今天仍旧有很多人不理解,或者不愿意理解。或许是认为相对论太难以理解了,或许压根就不愿意相信相对论。
网络上曾流传这样一句话:地球上理解相对论的人不超过三个。显然这种说法太夸张了。
事实上相对论并没有那么难,尤其是狭义相对论中的“时间膨胀”效应更不难。这里就同通俗的数学语言来解释时间膨胀,学过初中数学就能理解。
狭义相对论中有一个重要概念,那就是时间膨胀。简单来讲,速度越快,时间流逝的速度就越慢,当无限接近光速时,时间就会趋于停止。
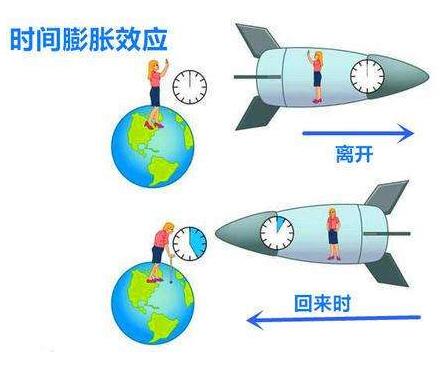
为何会这样?为何时间会和速度建立如此关系?在很多人的思维里,时间就是时间,速度就是速度,两者没有也不应该有关系。
而狭义相对论中的时间膨胀,是基于一个重要前提的条件下提出来的,这个前提就是:光速不变。
光速不变并不是说“光速在真空中的速度恒定30万公里每秒”,而是说“在任何参照系下,光速都是不变的”。
举个简单的例子,即使你乘坐99%光速飞行的飞船,在地球上的我看到你身上发出的光的速度仍旧是光速,而不是199%光速(光速+飞船速度)。
明白了这点,我们就继续开始数学诠释。
假设有一个非常精确的光子钟,这个光子钟结构非常简单,上下分别有两面镜子组成,间隔为15CM,镜子之间有一个光子来回运动,光子上下垂直运动。假设光子上下运动一个来回就是一秒。
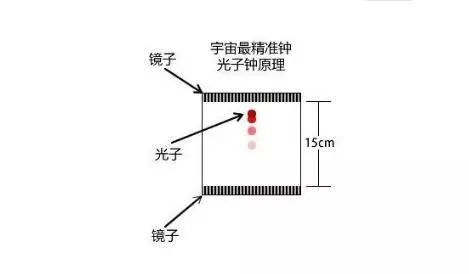
现在我们假设你拿着这个光子钟在宇宙飞船上快速飞行,我在地球上观察这个光子钟,会看到光子怎样运动呢?
显然,我会看到光子不再垂直上下运动,而会沿着斜线运动,原因很简单,因为宇宙飞船在快速飞行,光子上下运动的同时,还会受到飞船运动的影响。

也就是说,在我看来光子上下运动一个来回的距离变长了,意味着光子上下运动一个来回的时间不再是一秒,而会变得更长。
但是对于飞船上的你来讲,光子上下运动的一个来回的时间仍旧是一秒,因为在你看来光子仍旧是上下垂直运动,而不是斜线运动。
于是,相对我来讲,你的时间变慢(膨胀)了,我看到你的一切都变慢了,就像慢动作回放的电影那样。
到这里,道理我们都明白了,那么该如何用数学公式推导出来了?
很简单,勾股定律就可以做到了。
假设你所乘坐的宇宙飞船运动速度是V,你飞行的时间为t,你飞行的过程中地球上的我经历的时间为t’,如下图
利用勾股定律,很容易得出以下公式:c²t²+v²t’²=c²t’²(勾股定理)
通过简单的推导,最终就可以得出下面的公式:
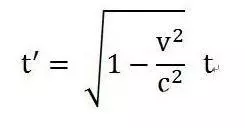
这就是时间膨胀公式。没想到会如此简单吧?
这个公式说明了什么?
如果你所在的宇宙飞船飞行速度V无限接近光速,意味着t会无限大,也就是说你的时间会趋于静止。而如果是另一个极端,也就是说V趋于零时,意味着t’和t趋于一致,其实就是我们非常熟悉的速度时间换算公式,也就是伽利略变换公式。而上面的公式就是洛伦兹变换。
可以看出,伽利略变换其实就是洛伦兹变换的特例,在低速世界下的近似值而已。
最后补充一点,狭义相对论除了时间膨胀(钟慢效应),还有质增效应(速度越快质量越大),尺缩效应(速度越快,距离越短),公式如下:
原文链接:https://www.toutiao.com/i7062672563897483815