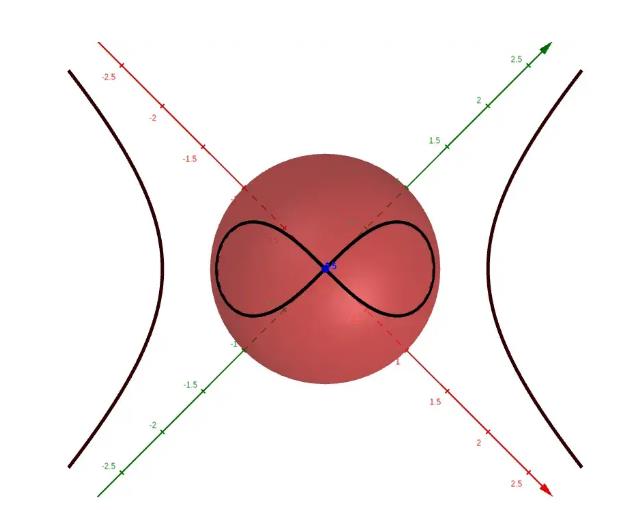
f(x) = 1/x 的立体投影
无穷大正在发生一些我们不完全理解的事情。
长期以来,物理学家一直在将有限值分配给无限发散级数(如果你愿意,可以是无限和),例如 1 + 4 + 9 + 16 + ⋅⋅⋅ ≃ 0 和 1 + 2 + 3 + ⋅⋅⋅ ≃ -1/12(你知道,那个几乎打破了互联网)。
这些无穷级数的结构非常严格,并与一个(复杂的分析)函数相关联,该函数以非常严格的方式使这些值成为唯一明智的选择,我们不会在本文中讨论。
当然,这些级数的真实评价(当我们将它们定义为极限时)是“无穷大”。然而,他们评估相同的价值或概念似乎并不正确,因为它们显然是非常不同的野兽。事实上,从渐近的角度来看,它们是不同的。尽管如此,它们还是趋向于无穷大!
但不知何故,当物理学家用这些值代替他们理论中的无穷大时,他们作为输出匹配实验得到的有限结果达到了惊人的数值精度。
从哲学上讲,这些总和几乎就像无穷大一样快,以至于它们“超调”并超出并回到数轴上。但这只有在数轴本身是圆形的(从拓扑学上讲)或者更一般地说,如果复平面是球体时才有意义。
在现实世界中,物理学家正在推测我们的 3D 空间是否真的是某个遥远的二维表面的投影。这被称为全息原理。是的,我知道这听起来如何,但他们有理由考虑这是一个很长(但很有趣)的故事……
以同样的方式,可以使用此(立体)投影构建一个与复平面(或通常的笛卡尔坐标系)平行的世界。
我们可以将平面(x, y)中的一个点,或者对于那些了解复数的人来说等效于x + yi ,作为在3D空间中有一个位于球体上的双胞胎,其中心为0,半径为1,因此是平面上的点和球体上的点之间的一一对应关系,除了我们将返回的球体上的一个点。
通过球化解决无穷大问题
在我们构建所谓的黎曼球之前,让我们先问一个看似简单的问题,世界各地的孩子们每天都会问他们的老师,即
“为什么我们不能除以零?”
可怜的老师想出了一些疯狂的答案,比如“因为你不能把你的披萨分成 0 个大小均匀的块”或更糟。事实上,实际上有几个原因导致我们不能以一致的方式除以零。
假设我们定义了一个实数 x = 3/0。然后两边都乘以 0,我们将得到 0 = 3,这当然是错误的。好吧,如果我们被允许除以零,结果就不可能是实数。好吧,让我们把它定义为无穷大,并将无穷大和负无穷大作为附加到实线的数字(这称为扩展实线,实际上是一个东西)。
好吧,很抱歉让你失望了,但这里也有问题。特别是,除法运算不再是连续运算,因为 0 是负实数和正实数之间的极限,从左边(在分母中)接近 0 会产生负无穷大,从右边接近 0会产生正无穷大。
我们解决这个问题的唯一方法是将负无穷大和正无穷大定义为相等。在那种情况下,我们将只有一个无穷大,我们的数字空间将不再是一条线,而是一个圆。这解决了连续性问题,我们实际上可以通过为所有实数 x 定义 x / 0 = ∞ 来理解被零除的意义。
这种方法也可以在平面上进行,但不是将无限线的两端粘在一起,我们需要把平面的整个无限“水平线”绑成一个点,有点像收紧一个边缘包。我们称那个点为“无穷远点”。这样,我们就得到了一个在无穷远处有一个特殊点的球体。
我们明确构造它的方式是通过一个从平面到单位球面的函数P。
想象一个数字平面,例如复数 ℂ 或通常的坐标系(或二维实数向量空间)ℝ²,以及一个以平面原点为中心、半径为 1 的球体。对于平面上的每个点 A,绘制穿过球体的北极N和A 的线。然后这条线将在第二个(唯一的)点α = P(A)与球体相交,这就是我们将A关联的点。
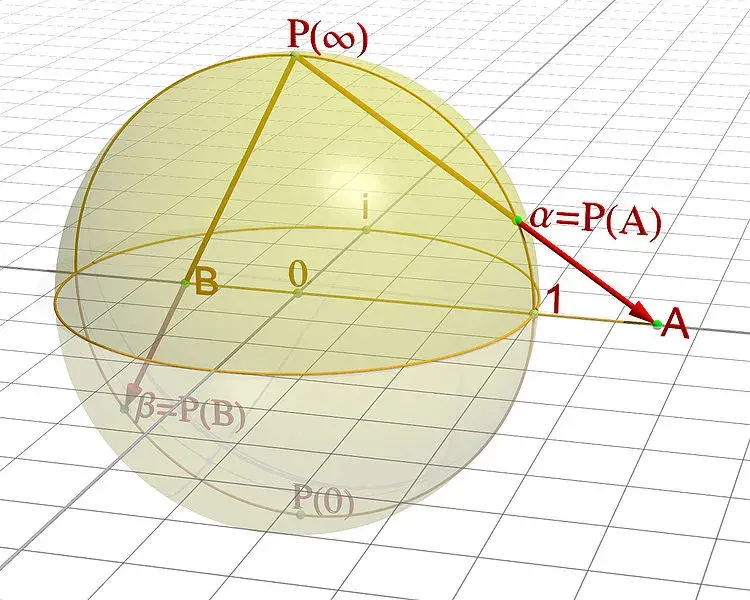
从平面到单位球体的共形映射
从这个结构中可以清楚地看出,用 |z| 指向 z > 1 映射到北半球并指向 |z| < 1 映射到南半球。平面中单位圆上的点保持原位。
还要注意,当我们在任何方向上越来越远离平面中心时,球体上的对应点越来越接近N。
虽然平面上没有映射到N的点,但我们可以在平面上到达无穷大的极限处击中它。所以我们说所有这些限制(与方向无关)映射到北极N——无穷远点。
对于感兴趣的读者,我们在这里有一个明确的 P 公式:ℝ² → ℝ³:
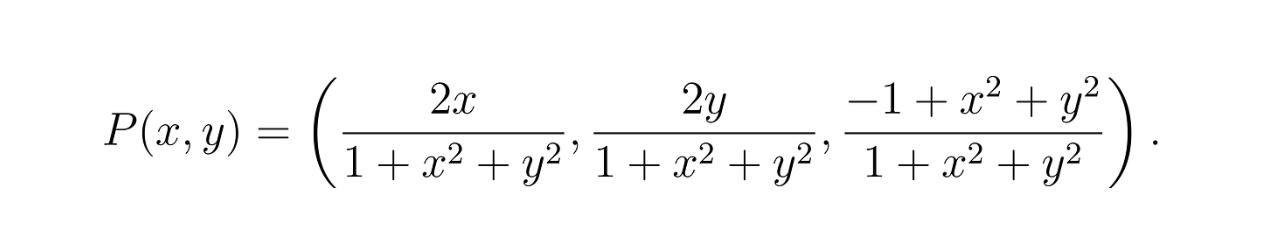
如果给定平面是复平面,则相应的球面称为黎曼球面或有时称为扩展复平面,因为它被视为集合 ℂ ∪ {∞}。映射P带有从复平面到球体的复结构,并且由于包含无穷大,球体上允许有极点,我们可以将亚纯函数视为黎曼球体上的全纯函数!
从没有北极的球体到平面的映射 P^(-1) 通常称为立体投影。
所以在这个空间中,我们可以除以零,因为北极是球体的一部分,并且f(x) = 1/x等函数在x = 0处是连续的。为了更清楚地看到这一点,我们将在下一节中考虑由 P 映射到单位球体的著名函数图。
球面上的实函数
让我们从最著名的函数开始:自然指数函数f(x) = e^x。我们有以下情节
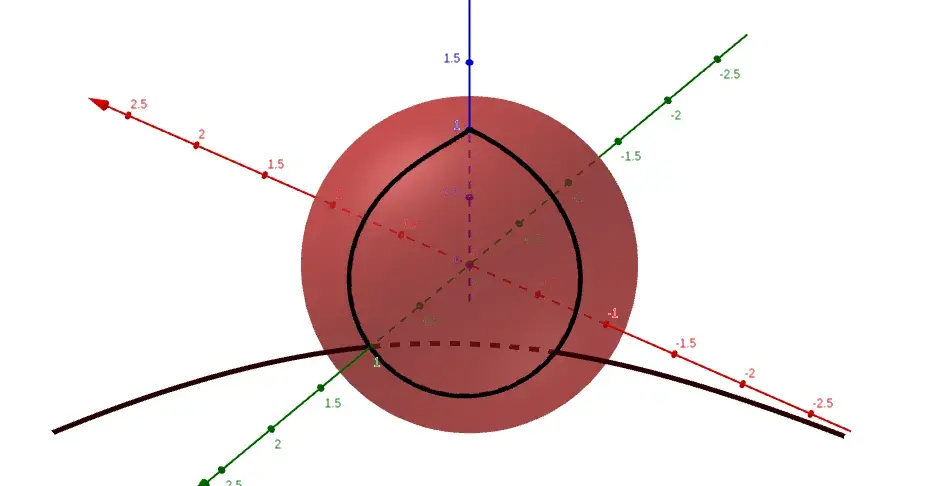
看看它把自己绑在一个循环中是多么美妙,因为图表的两端都达到了无穷大。这里红轴是x轴,绿轴是f轴。
从上方直视,我们可以清楚地了解形状,同时看到熟悉的情节!
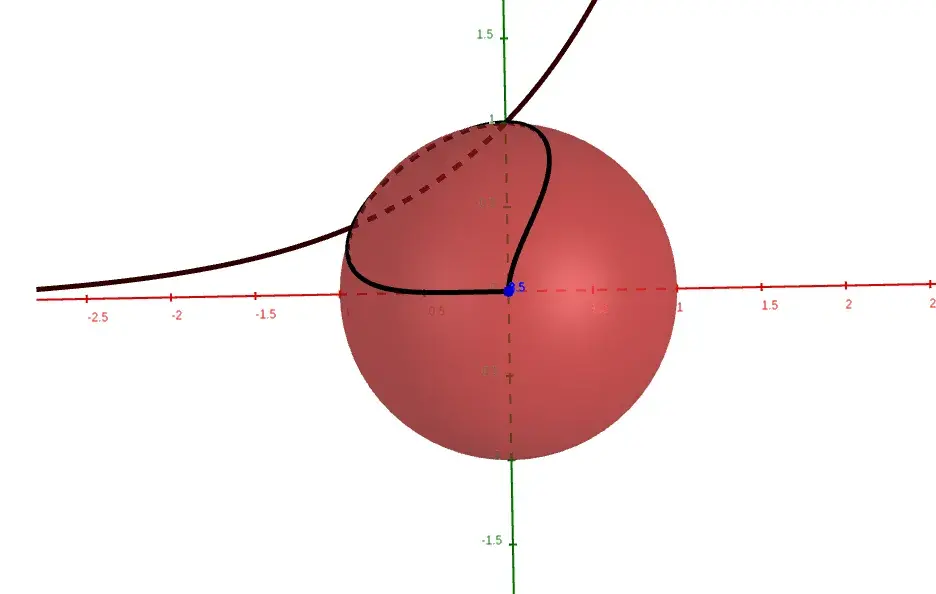
f(x) = e^x
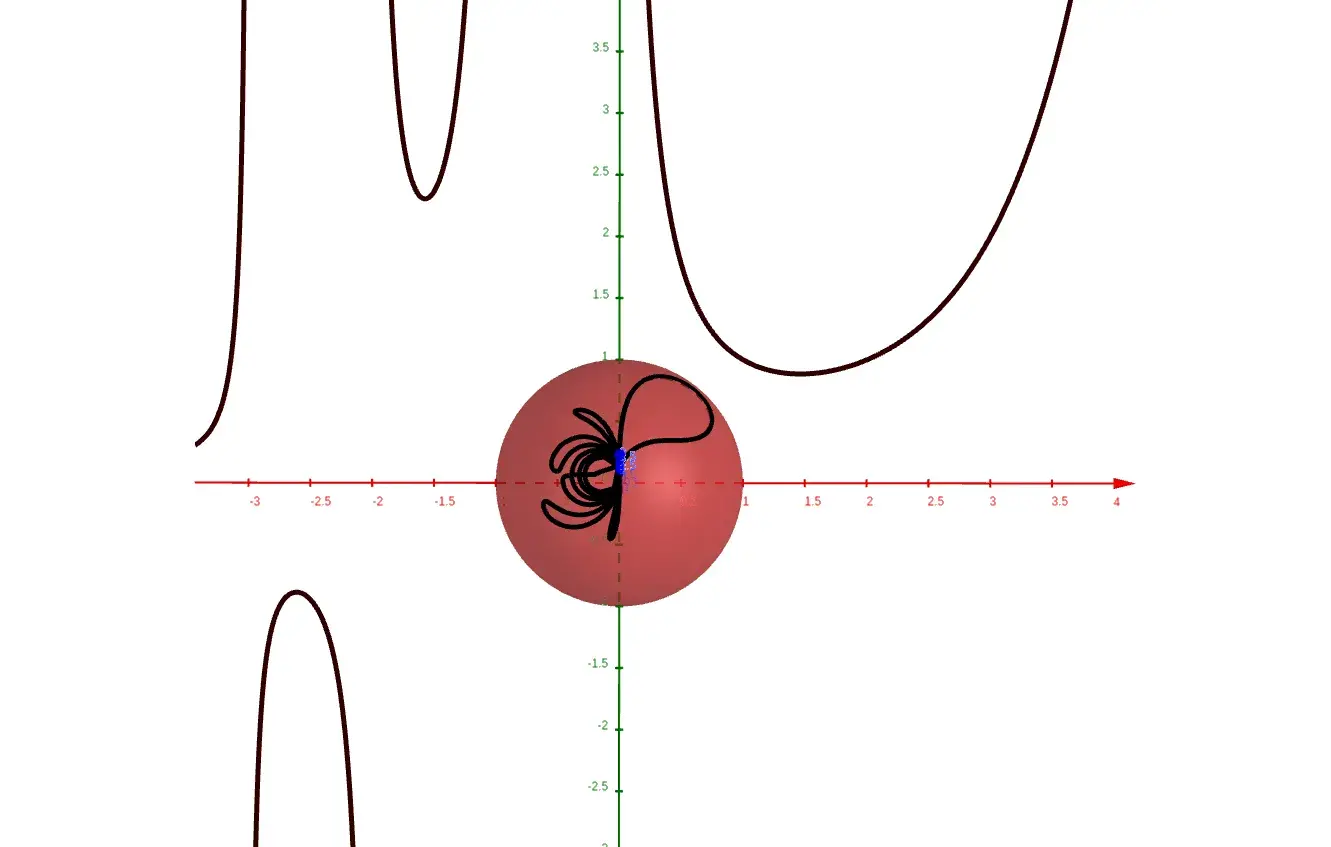
我们来看看麻烦制造者f(x) = 1/x定义为实函数时在 0 处不连续,即作为函数 f: ℝ\{0} → ℝ。这在球体上也有一条漂亮的闭合曲线。
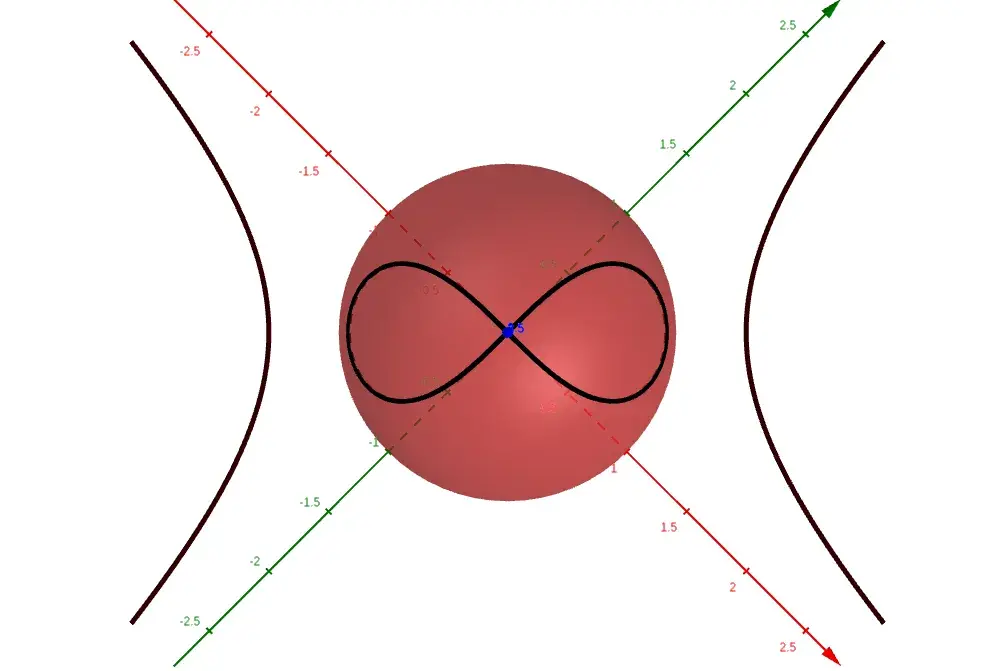
f(x) = 1/x
由于无穷大的问题,此函数在 0 处没有明确定义,但在球体上,它在 x = 0 处完美定义。诗意地,它形成了一个无穷大符号,这是数学蛋糕上的锦上添花。
常数函数怎么样?
此处绘制了函数f(x) = 2 :

常数函数只是球体上相交于无穷远的圆。对数怎么样?好吧,自然对数与球体上的指数函数具有相同的形状也就不足为奇了。
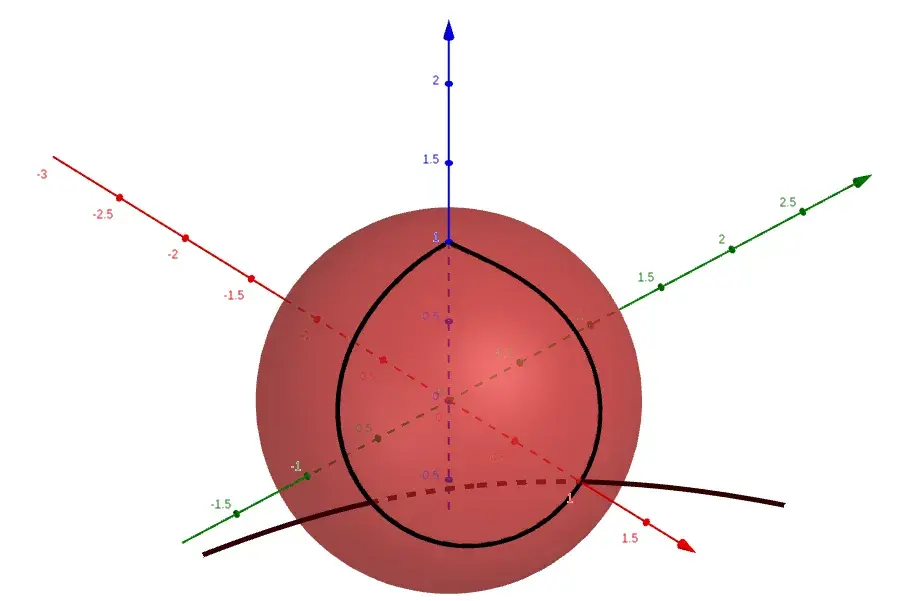
我们还有更多特殊函数图,例如伽玛函数Γ:
在本文中,我们探索了立体投影和黎曼球面的美丽世界。黎曼曲面有一个更一般的主题,我们考虑比球体更一般的形状,称为流形。它本身就是一个美丽而丰富的理论。
如果您想了解不同函数在球体上的外观,我在此处创建了以下可用的 Geogebra 表(
https://www.geogebra.org/calculator/nhnnpuqf)。您可能需要调整轴的长度和缩放比例以使其恰到好处。要尝试新函数,您只需更改 f(x) 的定义即可。尝试例如 f(x) = zeta(x)。