在探究自然界的微观宇宙时,我们遇到了诸多令人费解的现象,其中电子的行为尤为神秘。在传统的观念中,电子绕原子核的运动往往被比喻为行星绕太阳旋转的模式,然而,这种简化的比喻在量子力学的精确观测下显得过于幼稚。电子并非按照预定的轨道运动,它们存在于原子周围的“概率云”中,这意味着我们无法精确地预测一个电子在特定时间点的确切位置,而只能计算出它出现在某处的概率。

在量子力学的框架下,电子的这种表现是波粒二象性的直接体现,电子既有波的性质也有粒子的性质,它们的确切行为不是以可视化的轨迹呈现,而是以数学上的概率波形存在。量子力学通过波函数来描述这种概率,波函数的平方定义了在空间某处找到电子的概率密度。
进一步地,量子力学颠覆了我们对物质固有属性的认识。在经典物理学中,物体的位置和速度是清晰定义的,但在量子领域,海森堡不确定性原理告诉我们,位置和动量不能同时被准确知晓。电子的速度和位置的不确定性是根本的,不是因为测量技术的不足,而是自然界的基本性质。
这种难以直观理解的现象,是通过精确的实验测量得到的。早在20世纪初,光电效应和原子光谱的实验就暗示了电子的行为远远超出了经典物理的解释范畴。更进一步,现代实验技术,如电子显微镜和量子点实验,也提供了对电子概率分布的直接观测,这些实验不仅验证了量子理论的预言,同时也推动了我们对物质本质认识的深化。
因此,电子的“舞蹈”不是沿着简单的圆形或椭圆轨道,而是在由数学方程所定义的复杂几何空间中,以概率的方式展现其存在。这种理解方式虽然挑战了直觉,但却是我们目前对自然界微观层面最准确的描述。
经典理论的局限性
在深入量子世界之前,我们必须先理解过去的科学巨人是如何构建他们的原子模型的。19世纪末至20世纪初,物理学家通过实验和理论工作,发展了一系列原子模型,试图解释原子结构和电子的行为。其中最著名的是汤姆森的“布丁模型”和玻尔的太阳系模型。汤姆森模型将电子视为嵌入在正电荷分布中的小粒子,而玻尔模型则提出了一种假设,即电子在特定的轨道上绕原子核运动,且不会辐射能量。
玻尔模型在解释氢原子光谱方面取得了巨大成功,但很快人们就发现,它无法解释更重原子的光谱,也无法对多电子系统提供满意的解释。而且,根据经典电磁理论,绕核旋转的电子应该不断辐射能量,并最终坠入原子核,这显然与实际情况不符。原子的稳定性以及电子的非辐射旋转状态,无法在经典物理框架内得到合理解释。
此外,经典理论对于物质的固有属性提供了明确的描述,即每个物体在每一个时间点都有明确的位置和速度。然而,这种描述在原子尺度上遇到了问题。例如,光电效应实验表明,光必须被视为粒子流,这与经典波动理论相冲突。而康普顿效应进一步证明了光的粒子性,显示了经典理论在微观层面的不足。
由此,科学界意识到需要一种新的理论框架来描述微观粒子的行为,这最终导致了量子理论的诞生。量子理论不仅提供了一个全新的视角来理解电子的行为,而且也为我们打开了通向微观世界的大门,这个世界的规则迥异于宏观物体的经典物理规则。
从经典到量子,我们见证了科学理论的一个重大转折。这个转折不仅仅是科学理论的更新换代,更是对自然界深层规律认识的一次革命。只有放弃固有的、基于直观的预设,我们才能接受电子那些令人迷惑的量子舞蹈。
量子力学的兴起
随着物理学家们对经典模型的局限性认识的加深,20世纪初的物理学界开始酝酿一场革命,这场革命的中心是量子力学的诞生。量子力学的出现,不仅挑战了传统的物理观念,更为我们提供了一种全新的视角来理解物质的微观结构。
量子力学的核心思想是量子化。在这个理论中,能量不再是连续的,而是以最小的不可分割的单位存在,即“量子”。这一理念最初由普朗克提出,以解释黑体辐射问题。接着,爱因斯坦利用量子假设解释了光电效应,为量子理论的建立奠定了基础。
量子力学的发展是跨国界、多学科合作的成果。德国的海森堡首先提出了矩阵力学,几乎同时,奥地利的薛定谔发展了波动力学。虽然这两个理论从不同的数学形式出发,但后来被证明是等价的,它们共同构成了量子力学的数学框架。
量子力学提出了一个概念上的挑战:在微观尺度上,物质的行为和宏观物质完全不同。电子不再被视为行星一样围绕太阳旋转的小球,而是存在于一种既无法完全描述为波也无法完全描述为粒子的状态。这种行为无法用经典物理学中的路径概念来描述,因为它们不遵循确定的轨迹。
量子力学的另一个核心概念是波函数,它是一个数学对象,用于计算粒子在特定位置发现的概率。波函数的绝对值的平方,给出了粒子出现在某个位置的概率密度。因此,电子在原子中的行为不再是通过其位置和速度来描述,而是通过波函数来描述其概率分布。
量子力学不仅仅改变了我们对电子行为的看法,它也引领了现代科技的发展,从半导体技术到量子计算,量子理论无处不在。正是这个理论告诉我们,原子世界的确切描述只能通过概率和统计规律来完成,这一发现是现代物理学中最深刻的真理之一。
海森堡的不确定性原理
在探索量子世界的过程中,海森堡的不确定性原理是一个关键的里程碑。这一原理揭示了一个基本的真理:在微观尺度上,我们无法同时准确知道一个粒子的位置和动量。具体来说,一个粒子的位置和动量的不确定性之积,是有一个下限的,这个下限与普朗克常数有关。这意味着,任何尝试更精确测量一个量,都会使得另一个量的不确定性增加。
海森堡的不确定性原理对物理学界产生了深远的影响。它标志着对自然界认识的一个根本转变,即从绝对的确定性转向接受本质的不确定性。电子的位置和动量不是预先确定的属性,而是在观测的瞬间才决定。这与我们日常经验中宏观物体的行为截然不同,因为在宏观世界中,物体的位置和速度是可以同时准确测量的。
这个原理也直接关系到了电子在原子中的行为。由于电子的位置和动量不能同时被准确知晓,因此它们不能被描述为围绕原子核的确定轨道。相反,我们只能谈论电子在原子中出现在某个位置的概率。这个概率由电子的波函数来描述,而波函数的具体形式则由薛定谔方程给出。
从实验角度来看,不确定性原理已经得到了诸多实验的验证。例如,通过精确测量光子的散射来测量电子位置的实验,结果显示了位置的精确测量会导致其动量的不确定性增加。这些实验不仅验证了不确定性原理,而且还帮助我们更深入地理解了电子的量子行为。
海森堡的不确定性原理不仅是量子力学的一个基本组成部分,也是现代物理学的基石之一。它为我们提供了一个关于物质基本组成的全新视角,并且对于后续的量子场论和量子计算等领域的发展具有深远的影响。
薛定谔方程与波函数
海森堡的不确定性原理打开了量子世界的大门,而薛定谔的工作则提供了进入这个世界的地图。薛定谔方程是量子力学的核心,一个优美且强大的数学结构,描述了量子系统随时间演化的波函数。这个方程不是描述电子如何围绕原子核移动的轨迹,而是描述了电子存在于某个位置的概率。
波函数是一个复杂的数学对象,它包含了关于量子系统的所有信息。电子的波函数,特别是,描述了电子在三维空间中存在的概率云。当我们测量电子的位置时,波函数会“坍缩”,我们会在一个特定的位置找到电子,但在测量之前,电子的位置是不确定的。
这个描述不仅仅是理论上的;它已经通过无数次的实验得到了验证。电子干涉实验表明,电子确实表现出波动性,可以通过双缝实验中的干涉图样来观察。而当我们不观测电子的路径时,它们好像同时穿过了多个缝隙,表现出波的性质。
波函数的另一个奇妙之处在于其统计性质。由于它描述的是概率,因此它符合统计规律。电子的波函数不直接告诉我们电子在哪里,但它告诉我们在多次测量中,电子出现在不同位置的概率。这意味着,如果我们准备了很多相同的原子,然后测量其中的电子,我们会得到一个符合波函数预测的概率分布图。
波函数也反映了电子的能量状态。在一个原子内,电子的波函数取特定的形式,称为原子轨道。这些轨道对应于电子的能量级,而且每个轨道都有一个或多个电子的概率分布模式。
通过薛定谔方程和波函数,我们不仅能更好地理解电子的量子行为,还能预测和解释原子和分子的化学性质。这些性质在很大程度上决定了物质的结构和反应性,从而影响了整个化学领域的理解。

概率云模型
从薛定谔方程与波函数的讨论中我们知道,电子在原子中的行为是以概率形式存在的,而非确定的路径。这一现象在物理学中以概率云模型得到了形象的描绘。概率云模型是量子力学对电子在原子中位置分布的直观表达,它揭示了电子出现在原子周围某个特定区域的概率。
在概率云模型中,原子核被描绘为位于中心的点,而电子则不是以清晰的轨道存在,而是形成一个围绕原子核的模糊云。这个“云”的密度在不同区域是不同的,密度高的地方,电子出现的概率也高;密度低的地方,电子出现的概率也低。这种描述不仅适用于单个电子的原子,也适用于拥有多个电子的复杂原子,每个电子都有其自己的概率云。
这种模型的美妙之处在于,它为电子的量子行为提供了一个可视化的框架,尽管它不能像经典物理那样给出确定的轨迹,但它允许我们预测电子在空间中的分布。例如,通过计算氢原子中电子的概率云,我们可以得到一个关于电子在不同距离和方向上出现概率的详细图像。
在化学中,概率云模型具有重要的应用。化学家使用这个模型来解释和预测原子如何形成化学键,以及电子是如何参与化学反应的。电子的概率分布决定了它们能够与其他原子的电子云如何重叠,这种重叠是化学键形成的基础。
此外,概率云模型也有助于解释原子的性质为何随其在元素周期表中的位置而变化。例如,元素周期表中的趋势,如原子半径的变化、电负性和金属性的变化,都可以通过电子概率云的变化来理解。

量子态的叠加
在量子世界中,另一个引人入胜的概念是量子态的叠加原理。这个原理指出,一个量子系统的任何两个(或多个)可能状态都可以叠加在一起,形成一个新的状态。对于电子来说,这意味着它可以同时存在于多个状态,直到我们通过测量将其“坍缩”到一个确定的状态。
量子叠加是一个深刻且非直观的量子力学现象,它与我们在宏观世界的直觉截然不同。我们习惯于认为,一个物体要么在这里,要么在那里,但量子力学告诉我们,在微观层面,电子可以同时在这里和那里。这种可能性的并存是通过电子的波函数来表达的,波函数的不同部分可以代表不同的状态,并且这些不同的状态以概率的形式共存。
实验上,量子叠加的概念得到了充分的验证。最著名的实验之一是双缝实验,在这个实验中,单个电子似乎可以通过两个缝隙,与自身发生干涉,形成干涉条纹。这种行为表明,电子在没有被观测时,其波函数通过两个缝隙并在屏幕上形成叠加态。当我们尝试测量电子究竟通过了哪一个缝隙时,干涉图样消失,电子表现为粒子。
量子叠加不仅是理论研究的话题,它在实际应用中也起着关键作用。量子计算机的概念就是建立在量子叠加的基础之上,量子比特(qubit)可以同时存在于0和1的状态,这使得量子计算机在解决某些问题时比经典计算机更有效率。
在微观尺度上,电子的量子叠加也解释了原子和分子为何具有特定的能量级。这些能量级不是随机的,而是电子波函数允许的特定组合,这些组合决定了电子的能量状态。在化学反应中,电子的叠加态可以导致复杂的化学键形成,进而影响物质的化学性质。
原子轨道与能级
电子的量子态叠加为我们揭示了电子能级和原子轨道的存在。在量子力学的框架下,原子轨道不再是电子实际的运动轨迹,而是电子出现概率的空间区域。每个轨道对应一个特定的能量状态,这些状态是分立的,这就是我们所说的量子化能级。
原子轨道的概念源自量子力学对电子波函数的解释。在氢原子这样的单电子系统中,电子的波函数可以解析求解,而在多电子原子中,波函数变得更加复杂,需要使用近似方法。电子的波函数不仅决定了电子在空间中的分布,也决定了它的能量状态,因此,电子波函数的不同解对应着不同的原子轨道。
原子轨道的形状和大小直接影响原子的化学性质。例如,s轨道是球形的,电子在原子核周围的任意方向上被发现的概率是相同的。p轨道则有着偶数的叶片形结构,表示电子在特定方向上出现的概率更高。这些轨道的形状决定了原子如何与其他原子结合,形成分子或其他化学结构。
能级的概念也是解释光谱线的关键。当电子从一个能级跃迁到另一个能级时,会发射或吸收特定波长的光,这就是原子光谱线的来源。通过分析这些光谱线,科学家可以确定原子的组成和电子的能级分布。
在宏观层面,原子能级的分布影响材料的电导性、光学性质和磁性质。电子在不同能级间的跃迁决定了导体、半导体和绝缘体的特性。例如,半导体中价带和导带之间的能隙对其电学性质至关重要。

实验支持:从光谱到隧穿效应
量子力学的理论构建不是凭空而来,而是建立在坚实的实验基础之上。从早期的光谱分析到现代的电子隧穿效应,一系列实验不断地验证并丰富了我们对电子概率分布的理解。
光谱分析是研究原子和分子的一种重要手段。通过分析从原子发射或吸收的光的光谱,科学家们可以推断出电子的能级。这种分析揭示了电子并不是在原子核周围任意的位置,而是在特定的能级上。这些能级对应于电子波函数的特定解,进而形成了特定的概率分布。每当电子从一个能级跃迁到另一个能级时,就会发射或吸收一个特定能量的光子,这形成了光谱学中的线谱,这些线谱是量子理论预测的直接证据。
另一方面,电子隧穿效应提供了更直接的证据。隧穿效应是指电子能够通过一个看似不可能穿越的势垒,这是经典物理学所不允许的。这个效应在扫描隧道显微镜(STM)中得到了应用,该技术能够对单个原子甚至是单个电子的位置进行成像。STM通过探针和样品之间的隧穿电流来检测样品表面的电子概率云,这种技术不仅展示了电子的概率分布,而且还允许科学家们操作单个原子。
隧穿效应也是现代电子学中重要的概念,如在量子点和量子阱等纳米结构中。这些结构的电子状态被限制在非常小的空间区域内,允许电子的波函数形成新的量子态。量子点的特性是由电子概率分布的形状和大小决定的,这些性质可以通过改变量子点的尺寸来调节,从而在电子器件中实现新的功能。
这些实验不仅证实了量子力学的基本原理,而且还推动了新技术的发展,如量子计算和量子通信。电子概率分布的理解和操作是现代技术发展的关键,而这些都是基于量子力学的坚实实验基础。
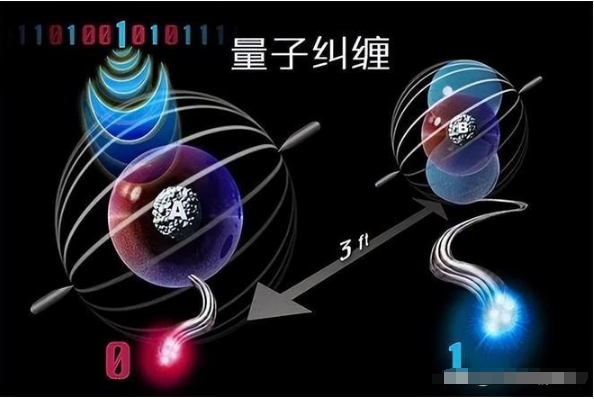
量子纠缠与信息传递
量子纠缠是量子力学中又一个非常不同寻常且迷人的现象,它揭示了量子世界中粒子间深层次的关联性。当两个粒子处于纠缠状态时,对其中一个粒子的测量将立即影响到另一个粒子的状态,无论这两个粒子相隔多远。这种现象超越了经典物理学的局限,甚至被爱因斯坦称为“幽灵般的远距离作用”。
在电子的语境中,量子纠缠意味着两个或多个电子可以以这样的方式关联,即对一个电子的状态的知识会给我们提供另一个电子状态的信息。这一现象在实验中得到了验证,如贝尔不等式的实验违背,证明了量子纠缠的真实性,这些实验结果显示,量子纠缠不仅是理论预言,它确实发生在物理系统中。
量子纠缠在量子信息科学中扮演着核心角色。量子计算机利用纠缠粒子来执行计算,这可能使量子计算机在处理特定问题时远远超过传统计算机的能力。量子通信也利用纠缠状态来传输信息,理论上这种通信方式是不可窃听的,因为任何尝试测量纠缠粒子的行为都会立即被检测到。
在探索电子的概率分布时,纠缠现象提供了一种理解和描绘电子之间相互作用的新方式。在多电子原子或分子中,电子不是独立存在的,它们之间的相互作用会导致复杂的纠缠状态,这些状态影响了物质的性质和反应。
纠缠也为我们理解量子态叠加提供了新的视角。电子的纠缠状态本身就是一种叠加状态,当我们测量其中一个电子时,系统的整个叠加状态都会受到影响。这种全局性的性质是量子力学与经典世界直观感受最大的不同之处。
量子计算与电子概率分布
量子计算是量子力学应用的前沿领域之一,它与电子的概率分布有着密不可分的联系。在传统计算机中,信息是通过二进制形式的“0”和“1”来表示和处理的,但在量子计算机中,信息单位是量子比特或qubit。每个qubit可以同时处于“0”和“1”的量子叠加态,这一性质来源于电子的概率分布原理。
量子计算的强大之处在于其并行计算能力。由于每个qubit可以同时表示多个状态,因此量子计算机可以在一个计算步骤中处理大量的可能性。这种计算能力使得量子计算机在解决某些类型的问题上,如整数分解、数据库搜索和模拟量子系统时,比传统计算机更加有效率。
电子的概率分布是实现量子计算的关键。在量子计算中,电子的波函数被用来编码和操纵信息。通过精确控制电子的量子态,量子计算机可以执行复杂的算法。这些操作依赖于电子态的叠加和纠缠,反映了电子波函数的概率本质。
量子计算的实现还依赖于量子态的精确控制和测量。为了在计算过程中保持量子位堆叠和纠缠状态,必须极其精确地控制实验条件,包括温度、磁场和电场等因素。这些条件直接影响电子的波函数和概率分布,因此量子计算的实现是对量子力学理论的深入应用。
此外,量子计算还需要维持量子态的相干性。在实际操作中,量子系统很容易受到外部环境的干扰,这会导致量子信息的丢失,这个过程被称为“量子退相干”。科学家们正在研究如何保护量子系统免受这种干扰,以实现实用的量子计算机。
量子计算不仅推动了计算科学的发展,也为物理学家提供了研究量子现象的新工具。通过模拟复杂的量子系统,量子计算机有望解开物质性质的许多未解之谜,这些都是建立在对电子概率分布深入理解的基础上。

结论 — 量子世界的未解之谜
在探索了电子的概率分布及其在量子力学中的深远意义后,我们现在回到了出发点,但带着更加深入的理解和数不尽的问题。量子力学为我们揭示了一个非直观且令人惊叹的微观世界,其中电子的行为远不如我们在宏观世界的日常经验那样直白。
电子不是简单地围绕原子核旋转的微小粒子,而是以概率云的形式存在,这个云是通过波函数的数学语言来描述的。电子的位置和动量的不确定性,以及它们的叠加状态和纠缠现象,都是量子力学的基本特征,这些特征指导着我们对自然界的理解和技术的发展。
量子计算机的概念和实验的验证,如电子隧穿效应和光谱分析,都是量子理论预言的实证。然而,尽管取得了这些成就,我们对量子世界的理解仍然是有限的。量子理论在解释某些现象时非常成功,但它也留下了许多未解之谜,比如量子引力和宇宙的量子描述等。
电子的概率分布对于现代科技至关重要,从化学到材料科学,从信息技术到基础物理研究,量子力学都在其中扮演着核心角色。它改变了我们对世界的看法,从确定性的机械宇宙观转向概率和不确定性的量子宇宙观。