数学中高耸的金字塔——拉格朗日

浏览 1296 · 点赞 0 · 评论 0 · 5年前 (2019-08-13)

对于十八世纪的数学界而言，欧拉无疑是最伟大的人物，而除去欧拉之外，最响亮的名字无疑是拉格朗日。作为法国数学著名的“三L”之首（其余二人为拉普拉斯和勒让德），拉格朗日为法国数学走向辉煌奠定了坚实基础。由于出众的贡献，拉格朗日颇受拿破仑的器重，并被这位高傲的皇帝称赞为“数学这门学科中高耸的一座金字塔”。

数学近两百年来的许多成就都可以直接或间接追溯到拉格朗日的工作上，而对于分析学及相关学科而言，他是整个数学史上最具影响力的几个数学家之一。

拉格朗日

拉格朗日的一生并不像费马那样波澜不惊，在自身的身世和性格，还有时代的影响下，他的一生颇具传奇色彩，甚至算得上跌宕起伏。

拉格朗日（Joseph-Louis Lagrange，1736~1813）尽管被后世称为法国数学家和力学家，但他实际上并不能算是一个完全的法国人。拉格朗日的祖父曾经是法国的骑兵，长期在意大利的撒丁岛上服役，退役后定居于意大利的都灵，又取了当地人为妻。拉格朗日的父亲虽然继承了自己父亲的职务和财产，但这位著名的败家子和投机分子很快就将财产挥霍一空。拉格朗日的父亲也许是天生不幸，他的十一个子女除了拉格朗日外全部夭折。不过拉格朗日回忆到自己的父亲时，却乐观地说到：“如果我真的继承了丰厚的财产，那么我很可能将与数学无缘”。这样的“不幸”对于拉格朗日本人和数学界而言，或许是一种真的幸运。

拉格朗日的青年时代都是在都灵度过的，按照传统，拉格朗日着重学习了欧式几何，阅读了欧几里得和阿基米德等古希腊数学家的著作，渐渐熟悉了来自古希腊的综合几何方法，不过几何学在拉格朗日的一生中从未真正引起过他的兴趣。

恰好在这个时候，英国著名天文学家哈雷写的一篇名为《论分析方法的优越性》的论文传入了拉格朗日的手中。在论文中，哈雷介绍了微积分理论在几何学上的应用，极力称赞分析方法相对于欧式几何的优越性。分析学就这样一下子引起了年轻的拉格朗日的兴趣，成为了他一生研究的中心。

在非常短的时间里，拉格朗日就通过自学掌握了当时几乎所有的分析学知识。大约在18岁的时候，拉格朗日写出了自己的第一篇数学论文，研究了如何用牛顿二项式定理得出函数乘积的导数。不过这一结果早已经被莱布尼茨获得，也就是我们熟悉的莱布尼茨公式：

拉格朗日非常兴奋地写信给欧拉告诉他自己的成果，尽管这已被前人发现，但欧拉还是看出了拉格朗日巨大的潜力，于是回信鼓励了这位年轻人。幸而拉格朗日并没有垂头丧气，反而愈发奋进，成为了欧拉之后最出色的分析学家。

变分法与微分方程

在欧拉的影响下，拉格朗日开始研究当时非常热门的变分法。变分法起源于最速下降曲线问题，这个问题最早由约翰-伯努利提出，而后首先被伟大的牛顿所解决。欧拉作为伯努利家族的继承人，对变分法可谓情有独钟，他于1744年出版的著作《寻求具有某种极大或极小性质的曲线之技巧》则正式标志着变分法这门学科的诞生。

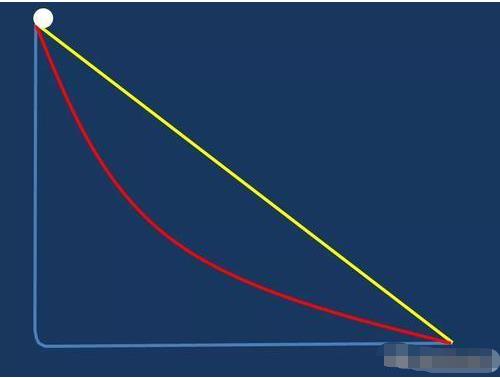
拉格朗日在研究“等周问题”的过程中，他充分领会了欧拉的变分法思想，完全摒弃了伯努利兄弟那种模糊不清的几何观点，代之以可靠的分析方法，从而完全解决了这个了古老的问题，同时他也为变分法奠定了分析学的基础，提出了所谓的变分法基本引理。1775年，拉格朗日发表了题为《论确定不定积分公式的极大和极小的一个新方法》，清晰地阐述自己关于变分法的分析方法，给出了一类适用范围非常广泛的一个变分问题的系统解法，这个问题就是求满足一定条件的函数，使得下列积分取极值。

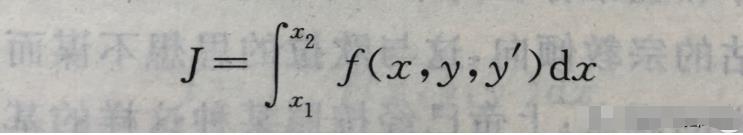
而且，拉格朗日对变分法的探索并没有止步，他还继续研究了被积函数包含高阶导数和多重积分的情形。更重要的是，他成功把变分法引入到了力学之中，例如他首先用具体形式正确表达了最小作用原理。拉格朗日关于变分法的研究成果如今都成为了教材中的标准内容。

在变分法上的贡献使得拉格朗日名声大噪，风头一度盖过了欧拉，这使得他在19岁的时候就当上了都灵皇家炮兵学校的数学教授。在校期间，拉格朗日积极组织有才华的年轻人一起讨论，几年后将众人的成果结集出版为《都灵论文集》。而且他还解决了当时颇具争议的弦振动的方程问题，成功给出了正确的数学表达式，拉格朗日也从这里走上了微分方程的研究之路。

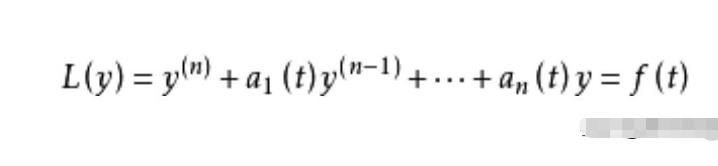
在研究不定系数常微分方程的过程中，拉格朗日引入了如今所称的“伴随方程”这个重要概念，并且证明了一系列关于奇解和通解的重要结论，指出了它们之间的重要关系。这些关于常微分方程的理论如今也构成了相关教科书的标准内容。同时，拉格朗日也是一阶偏微分方程理论的开创者，他建立起了一些关于偏微分方程的初步理论，这些理论后来被柯西发扬光大。

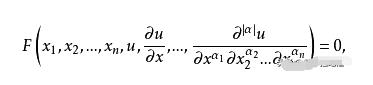
由于在分析学上的贡献实在太耀眼，拉格朗日在年仅23岁之时就当选为柏林科学院的通讯院士，一跃成为欧洲最一流的数学家。

天体力学与分析力学

在拉格朗日的时代里，数学分析只是被当做研究几何或力学的数学工具，而拉格朗日又对几何不感兴趣，那么力学就成为了他发展分析学所离不开的学科。事实上，力学方面的成果几乎占据了拉格朗日整个研究成就的一半。与前人不同的是，拉格朗日决不把数学看成是物理的附庸，而是力主把数学和力学等学科分离开来，通过完善数学理论来促进力学的发展，而他在天体力学和分析力学上的成就充分证明了自己的思想是多么正确。

1764年，拉格朗日利用万有引力定律成功解释了月球天平动问题，一举斩获重量级的巴黎科学院大奖，这也是他对力学思考后的第一个成果。两年之后，拉格朗日再次获得巴黎科学院大奖，这次的成果是关于更为复杂的木星四卫星问题。这样的荣誉可能和如今得两次诺贝尔奖差不多，不过雄心壮志的拉格朗日对力学的期望远不止此，他要寻找一套关于力学的普适方法，就像天体力学中的万有引力定律一样，这些思考的结果总结在了后来的巨著《分析力学》之中。

对于当时的天体力学而言，拉格朗日既不是第一人，也不是成就最大的（集大成者当属拉普拉斯），但对于分析力学而言，拉格朗日无疑是“上帝”一般的人物，仅仅是一个拉格朗日方程，便足以让他名留青史。

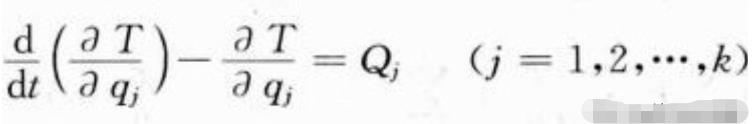
1766年，自诩为“欧洲最伟大的国王”的普鲁士国王腓特烈二世为了满足自己“欧洲最伟大的宫廷要有最伟大的数学家”这个愿望，在欧拉和达朗贝尔的引荐下，邀请了拉格朗日来到柏林科学院工作。拉格朗日一下子成为了欧拉的同事，而且这一待就是二十年，直到腓特烈去世。作为一个外国人，拉格朗日在古板的德国人包围下，过得并不太愉快，但这丝毫没有影响他的研究热情，而实际上，拉格朗日一生最重要的成就几乎都是在这段时间里完成的。

达朗贝尔

在拉格朗日之前，受牛顿和伯努利兄弟的影响，对力学的研究都非常依赖于几何直观，但实际上这是一个沉重的枷锁。受欧拉的达朗贝尔的启发，拉格朗日的想法则是完全摆脱几何上的直观，代之以可靠的分析方法，这与他在变分法上思想完全一致。这些思想和成果都总结在了《分析力学》一书中，全书以变分法为基础，突出分析方法，将力学中的关系全部数学化，从而建立起了一套优美和谐的力学体系。书如其名，全书没有任何一幅图，只用了数学分析的方法，故此拉格朗日甚至直言：

力学已经成为数学分析的一个分支！

方程与数论

尽管拉格朗日以分析学上的成就著称，但他在代数和数论上的成就在历史上也占有一席之地。在《关于解数值方程》和《关于方程的代数解法的研究》两篇论文中，拉格朗日提出了“方程的预解”和“根的置换”这样的概念，这实际上已经蕴含了置换群的思想。这样的思想最终被伽罗瓦和阿贝尔继承，并最终彻底解决了一般高次方程无根式解这一千年数学难题。

一般五次方程：ax^5+bx^4+cx^3+dx^2+ex+f=0（a,b,c,d,e,f为常数，x为未知数，a≠0）

同时，拉格朗日在数论上的贡献也不容小觑。首先他证明了费马所遗留的两个难题：

证明一个正整数可以表示为不超过四个平方数之和；

求不定方程x^2-Ay^2=1的整数解，其中A为非平方整数。

拉格朗日不仅解决了这些即使在欧拉手里也无能为力的难题，更重要地，他还提出了解决这些问题的基本理论，同时也对原问题进行了推广，甚至考虑了更一般的情形。除此之外，他还证明了：

圆周率π是无理数；

n是素数的充要条件为(n-1)！+1能被n整除。

巴黎

普鲁士国王腓特烈二世在1786年去世，此时欧拉也已经去世，拉格朗日一下子失去了靠山，在柏林成为了受排斥的“异乡人”，于是在法国国王路易十六的邀请下，他最终回到了自己的祖国，定居于巴黎，直至去世。身心俱疲的拉格朗日自感已无力再从事难题的研究，但偏偏又碰上了大革命，这又再次激发了他的创作热情。尽管为旧王朝服务过，但革命派和拿破仑非常赏识和敬重拉格朗日的才华，这使得拉格朗日不仅免遭像拉瓦锡那样被砍头的噩运，而且还被委以重任，在新成立的巴黎高师和综合工科大学任教。

尽管这一时期拉格朗日没有出色的研究成果，但他还是完成了许多重要工作。1799年，在拉格朗日的领导下，巴黎科学院完成了统一度量衡的伟大创举，提出了今天我们所使用的诸如十进制的米制单位等。比较有意思的是，当时有不少人想采用十二进制，但在拉格朗日的坚持下，最终还是采用如今广为使用的十进制。

此外他还编写了著作《解析函数论》和《函数计算讲义》等，阐释了自己对一般微积分理论的思考，我们非常熟悉的拉格朗日中值定理和拉格朗日插值公式就首次出现在这些著作中。但囿于时代的限制，拉格朗日刻意回避“极限”这个概念，因此他并没有真正解决微积分的本质问题，而“分析的严格化”这项划时代的工作将由柯西和魏尔斯特拉斯等后人所彻底完成。

生前身后

整个十八世纪的数学为欧拉和拉格朗日所支配，在拉格朗日还活着的时候，他就被尊称为欧洲最伟大的数学家，拿破仑更是亲封他为伯爵，由此可见他在数学史上的地位有多高。我们常常赞誉欧拉为“分析的化身”，而作为欧拉思想的真正继承人，拉格朗日完全算得上是“分析二世”，而事实上，他在很多方面都超越了欧拉，至少在分析和力学上是如此。因此我们看到，拉格朗日无愧为近代数学史上最具影响力的数学家之一。