布朗运动是指悬浮在液体或气体中的微粒所做的永不停息的无规则运动。它最早是由罗伯特-布朗在19世纪描述的,当时他观察到小的花粉颗粒以颤抖的方式移动。这种运动已经成为一个深入研究的课题,并导致了整个科学的众多进步。
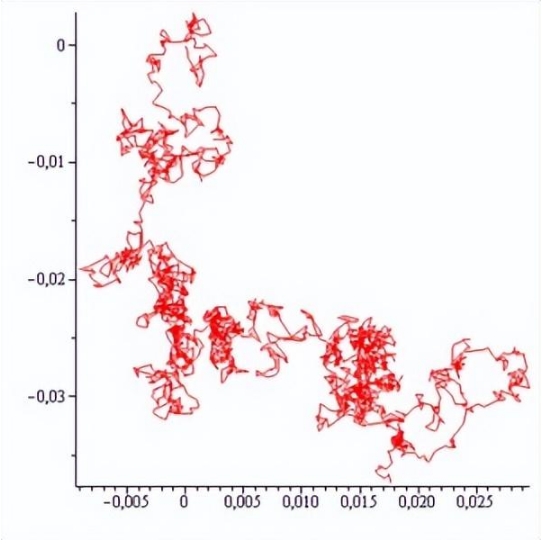
当罗伯特-布朗描述这种运动时,气体的动力学理论正在发展中,该理论将气体描述为一群随机地相互碰撞的粒子。当我们观察到越来越多的这种随机相互作用时,温度和压力之类的量就开始出现了。
进入20世纪后,这种理论仍有争议,统计力学也没有被完全接受。然后,爱因斯坦出现了。他在1905年和1908年发表了两篇论文,将布朗运动正式化,并布置了具体的实验来证明气体的动力学理论是真实的。这些实验是由让·巴蒂斯特·佩林( Jean Baptiste Perrin)完成的,他验证了爱因斯坦的理论,并证明了气体动力学理论的准确性。佩林因为这个实验在1926年获得了诺贝尔物理学奖。
这是物理学的一个重大发展,对我们对宇宙的理解产生了巨大影响。到目前为止,我只笼统地谈了布朗运动。如果能有一些具体的方程来谈,那就更好了。不幸的是,爱因斯坦的描述并不容易理解。我们将使用保罗-朗格文的理论,他声称他的推理是 “无限简单的”。

保罗-朗格文。
朗温做了很多工作。他的贡献包括提出 “孪生佯谬”,利用超声波定位潜艇的专利,以及在顺磁性和抗磁性方面的大量工作。他还因与玛丽-居里有染而受到议论(她是寡妇,但他是已婚)。在这篇文章中,我们将看一下他对布朗运动的正式描述的推导。
郎之万从以下方程出发,这是统计力学的一个结果。
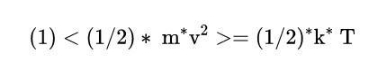
其中m是质量,v是速度,k是玻尔兹曼常数,T是温度。请注意,符号”<>”表示我们在取平均量。这个方程适用于一定体积的气体,所以左手边是该气体中每个粒子的平均值。
现在,让我们挑出一个质量为m的特定粒子。我们发现有两个力作用于它。第一个是阻力,我们用-F*v来表示,其中F是一个常数,取决于粒子(我们假设F对每个粒子都是一样的),v是速度。第二个是由B给出的,它代表粒子的随机 “波动”。我们假设B的平均值是0。
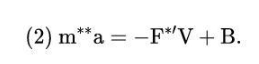
如果你把每项都乘以x,然后用乘积法则做一些变换,你会得到下面的方程式。
试着自己推导一下吧。
现在,取每个项的<>。也就是说,对我们体积中的每个粒子进行平均。得到了:
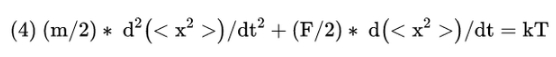
我做了一点整理,但也注意到B*x项没有了。为什么我们可以消掉它?之前我说过,我们假设B的平均值是0。这意味着当我们观察体积中每个粒子所经历的随机碰撞时,它会被抵消掉。因为我们假设一个粒子所经历的随机波动(B)与它的位置(x)没有关系,这是一个很大的假设,其他人已经在没有这个假设的情况下完成了这个推导。
这个方程是可解的。我们来求<x>的一次导数的解。我得到
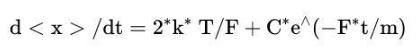
其中C是任意常数。朗之万指出指数项是无关紧要的。去掉这一项并求解<x>得到解:
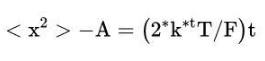
其中<x^2>的初始值为A。这是一个非常强大的方程!它使我们能够估计 “扩散 “的程度。它允许我们纯粹通过了解气体的温度(T)和粒子的微观属性(F),来估计气体是如何“扩散”的。布朗运动是一个令人难以置信的工具,它使我们能够将微观运动与宏观动力学联系起来!推导出这个方程是至关重要的。推导出这个方程是理解随机过程的关键步骤。
这个解也非常类似于我在这篇文章中描述的 “随机波动 “情况,但它反而被应用于理想化的气体。
如果你有兴趣阅读更多关于布朗运动的文章,我强烈推荐这本书。我是从这本书中得到这个推导的。你会发现,即使在第一章,这些想法也可以进一步得到非常有趣的结果。
