人类生活在一个被称作三维空间的世界中,但我们的感知和理解能力真的能触及这个空间的全貌吗?事实上,人类的大脑和感官在本质上是二维的,这限制了我们对更高维度空间的直观理解。
人的视网膜是二维的,它只能捕捉到平面上的信息。当我们观察一个三维物体时,视网膜上得到的其实是这个物体的二维投影。
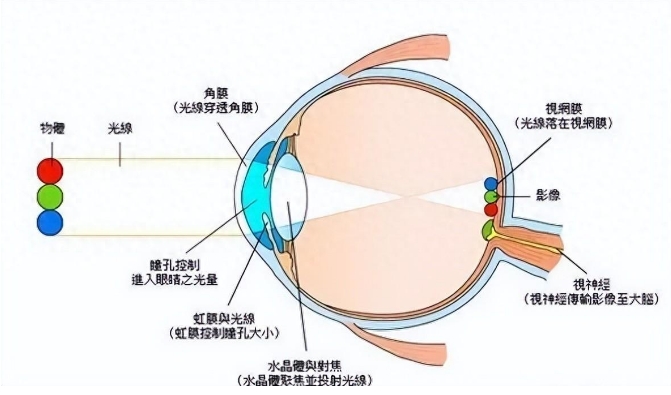
尽管如此,我们仍能感受到物体的立体感,这是因为立体视觉的原理。我们的左右眼位于同一平面上,略微不同的视角使得左右眼捕捉到的图像有所差异。大脑将这两张二维图像叠合在一起,通过差异对比和空间推理,我们就能感知到立体的三维形象。
然而,这种立体感本质上是一种视错觉。例如,三维电影就是利用这一原理,通过计算机技术在二维的银幕上创造出三维的视错觉。
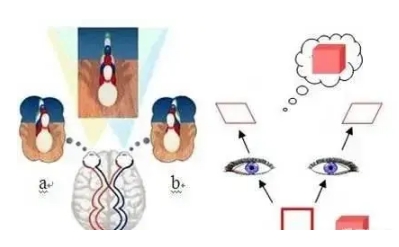
观众佩戴的立体眼镜使得左右眼看到不同的图像,从而在大脑中合成出一个虚拟的三维空间。尽管如此,我们的大脑仍然无法真正理解和想象超出三维的空间结构。
尽管人类在三维空间中生存,但我们对这一空间的认知存在显著的误区。立体投影的幻象使我们以为能够看到真实的三维,但实际上我们只能通过二维的视网膜来感知世界。画家可以通过巧妙的绘画技巧欺骗我们的眼睛,创造出看似立体的二维图像。同样,机械工程师在设计和制造三维物体时,也需要将它们拆解为二维来理解和操作。
人类对空间的认知主要由生存和繁衍的需求驱动。在进化的历史长河中,那些能有效地在三维空间中导航和生存的个体更有可能繁衍后代。因此,我们的空间感知能力在很大程度上是为适应现实世界的基本需求而优化的。

对于超出这一需求的高维空间,我们的大脑并没有足够的激励去理解和探索。这就解释了为什么尽管我们生活在三维空间中,却很难真正掌握它,更不用说想象四维或更高维的空间了。
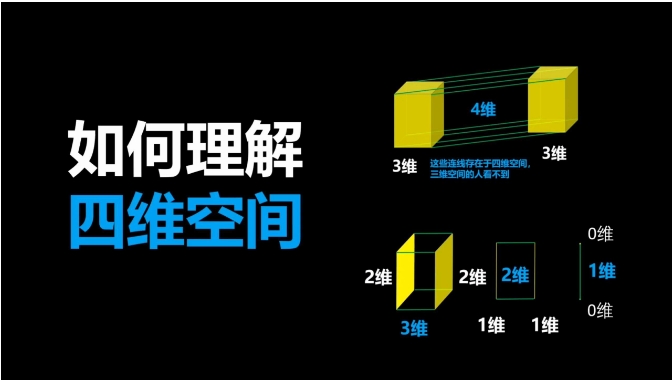
四维空间的复杂性超出了人类基于二维感官和三维经验的直观理解。数学和几何学为我们提供了探索高维空间的工具,但我们很难将这些抽象的数学概念转化为具体的空间形象。例如,数学家使用坐标系和公式来描述四维或更高维的空间,但这些描述对于大多数人来说仍然是难以想象的。
我们可以尝试从四维生命体的视角来理解四维空间。假设四维生命能够直接感知四维物体,它们可能会通过三维投影来观察世界,就像我们通过二维视网膜感知三维世界一样。这种投影会将四维物体展现为三维的形态,而四维生命的大脑则能够解读这些投影,从而理解四维空间的全貌。然而,人类的大脑并未进化出理解四维或更高维空间的能力,因此我们无法直接体验这种投影。
尽管如此,人类的想象力并未因此受限。我们可以通过数学和几何的帮助,至少在理论上探索四维空间的可能性。
例如,卡拉比-丘成桐空间的发现就是一个突破。这一六维空间的数学模型虽然难以直观理解,但它的存在证明了高维空间不仅是数学上的抽象,也可能具有物理上的现实意义。这一发现激发了我们对空间认知的进一步思考,也为未来的科学研究提供了新的方向。
在探索高维空间的过程中,人类的想象力遇到了边界。一般人很难想象一个拥有四个或更多维度的空间,这超出了我们日常经验的范畴。对于大多数人来说,高维空间是一个抽象而神秘的概念,难以用常规的视觉或空间思维来把握。
然而,数学家们展示了一种与众不同的思维方式。他们不仅能够理解复杂的数学公式,还能通过这些公式来想象和描述高维空间。
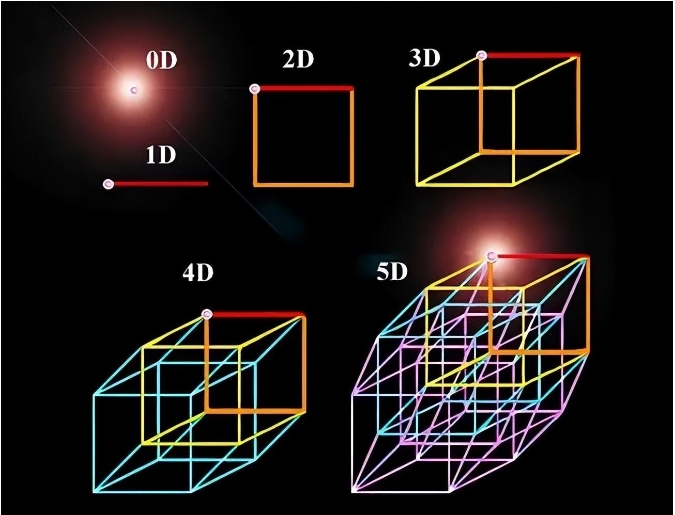
这种能力让数学家能够探索并证明高维空间的存在,即使这些空间在我们的直观感知之外。例如,卡拉比-丘成桐空间就是一个典型的例子。几何学家卡拉比提出了这一高维空间的猜想,而丘成桐则通过数学证明了它的存在。这一空间的发现是数学领域的一个重大突破,它表明高维空间不仅是理论上的构建,而且在数学上是真实可行的。
进一步地,数学家们甚至能够将这些高维空间的特性可视化。尽管我们无法直接看到这些高维空间,但通过数学模型和计算机图形学的帮助,数学家们可以将这些空间投影到我们的三维世界中,让我们至少能够在视觉上感受到高维空间的存在。卡拉比-丘成桐空间的雕塑展示就是一个令人印象深刻的例子。这个雕塑将六维空间的一小部分以三维的形式呈现出来,虽然它无法完全展示高维空间的全貌,但给了我们一个直观感受高维结构的机会。