本文,将会通俗阐释几个有关量子力学的“神奇实验”,这些实验均已经被实际验证,并且结果都证实了量子力学的“预言”。
这里只简述实验的过程和原理,并对实验现象与量子力学进行了关联性解读,相信这些足以让我们感性、深刻、细致地认识到,微观世界的不可思议。
主题目录如下:
实验:贝尔不等式
实验:单电子双缝干涉
实验:观察者双缝干涉
实验:光子延迟选择
实验:量子擦除
实验现象的各种解释
结语
实验:贝尔不等式
贝尔不等式是一个数学原理,如果不等式成立——则量子力学就是不完备的,如果不等式不成立——则量子力学是完备的。
而贝尔不等式,其数学推导成立的前提是:隐变量存在 + 定域性存在。
隐变量存在的意思是,存在未知变量可以避免“真随机性”,即:量子的不确定性,其实是没有观测到的一些“未知变量”所导致的。
通俗地说,就是物质的状态是独立不受观测影响的,因为“观测影响”被归结于隐变量,所以隐变量存在,也意味着物质状态的实在性,否则物质状态受观测影响,就不具有实在性。
定域性存在的意思是,存在信息传递不能超光速的限制,让物质之间的影响,必须经过局域空间并需要时间,因此定域性又称局域性。
通俗地说,就是物质之间的相互作用有先后顺序,所以定域性维护了因果关系的存在,否则没有先后顺序,就无法判断谁是因谁是果。
事实上,量子纠缠的超距作用就是违反定域性的,因为量子纠缠,是全局瞬间不需要时间的协调,尽管它不能传递信息,但却传递了“影响”。
可见,如果贝尔不等式成立,则意味着微观既没有不确定性(叠加态),也没有量子纠缠(纠缠态),即:量子力学是不完备的——也就是存在未知理论,可以解释上帝骰子与超距作用。
而通过实验,就可以验证贝尔不等式是否成立(即验证量子力学的完备性),实验可以使用电子自旋,也可以使用光子偏振,下面使用光子偏振,来简化阐释实验的过程和原理。
需要注意的是,贝尔不等式是一个(纯逻辑的)数学原理,它不针对任何物理模型与任何微观粒子,它的成立条件(即推理基础)仅是隐变量与定域性的同时存在,只不过物理实验可以验证它是否成立,从而让我们可以判断出,其“成立条件”是否存在。
实验前提
制备一对孪生光子,一个向左飞,一个向右飞,在测量之前并不知道光子的偏振方向,而根据能量和动量守恒,两个光子的偏振方向应该一致,也就是说,只要测量一边光子的偏振方向,另一边光子的偏振方向不用测量,也就确定了,即:两边偏振一致。
注意,这里是孪生光子对,不是纠缠光子对,纠缠光子对的偏振是相互垂直不一致的。
偏振(Polarization)——是指横波在垂直于波的传播方向上,存在朝着某一方向振动的性质。
然而上述结果,会存在两个可能的过程:
第一,出生确定,即孪生光子出生的时候,两者的偏振方向就已经确定,且两者之间没有关联。
第二,观测确定,即光子的偏振方向直到测量才确定,且两者之间有关联,也就是测量一个会影响另一个。
那么,到底是出生确定,还是观测确定呢?请看实验过程。
第一步
如下图所示,火柴棒即是光子,火柴棒的旋转方向即是偏振方向,左边女孩与右边男孩,各有一个检偏器可以让特定偏振方向的光子通过:如果光子通过记录1,不通过则记录2。
检偏器——是由偏振片(Polarizer)组成的检测设备,它可以检测光的偏振方向。

来自《量子之谜》(Quantum enigma)
那么,由中心向两边飞出大量孪生光子,男孩与女孩各自记录1或2,统计结果显示,两边的记录始终保持一致,即:一对孪生光子,如果左边通过女孩的检偏器——记录1,那么右边也会通过男孩的检偏器——记录1;如果左边不通过检偏器——记录2,那么右边也会不通过检偏器——记录2。
所以,记录一致的意思就是,每一对孪生光子在两边产生的记录,是对应相同的,即:记录1对记录1,记录2对记录2。
第二步
如下图所示,将女孩的检偏器,向左旋转θ角度,重复第一步的操作。
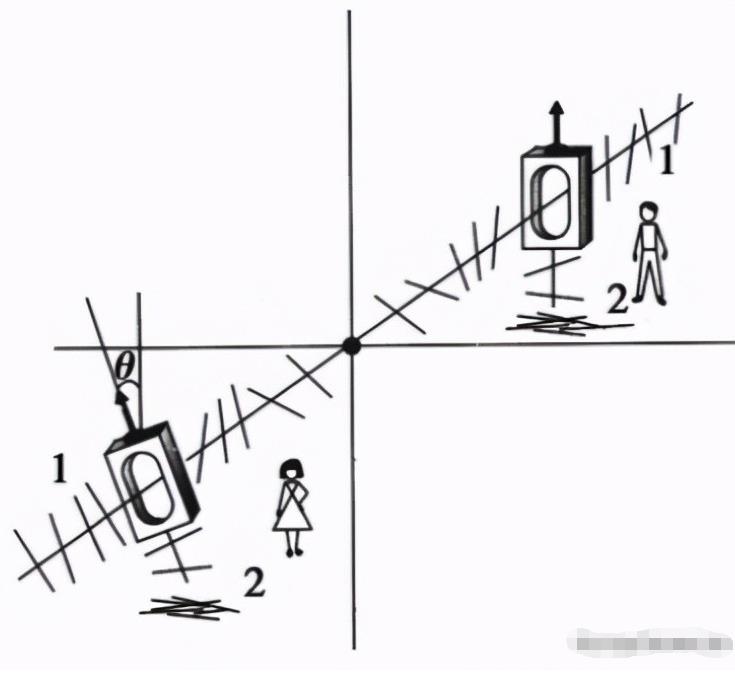
来自《量子之谜》(Quantum enigma)
那么,两边的记录就会不一致,因为有些男孩「记录1」的光子,对应到女孩这边的孪生光子,由于检偏器旋转θ角度而无法通过,结果成为了「记录2」的光子,于是就形成了——「记录1对记录2」这样的错配。
我们设置,检偏器θ = 30度,结果实验统计的错配率(即不一致的比例)约为25%,也就是说,在男孩与女孩的记录对比中,「记录1对记录2」的比例约为25%——这也可以理解为,旋转角度让25%的光子无法通过(只要偏振方向与检偏器不是垂直,就会有光子通过的概率)。
根据量子力学的公式,检偏器旋转θ角度,通过的概率是cos^2(θ)——因为垂直方向是通过 ,不通过的概率是sin^2(θ) ——因为水平方向是不通过,那么错配的概率就是:sin^2(θ) => sin^2(30°) = 0.5^2 = 0.25 = 25%,即不通过的概率。
第三步
重复第二步实验,只不过将男孩的检偏器,向右旋转θ角度,女孩的不旋转。那么,两边的记录同样也会不一致,即出现「记录1对记录2」的情况。
我们依然设置,检偏器θ = 30度,结果实验统计的错配率也是25%。
第四步
关键的操作来了,我们将男孩与女孩的检偏器,同时反向旋转θ角度,即:左边女孩的左旋θ角度,右边男孩的右旋θ角度。
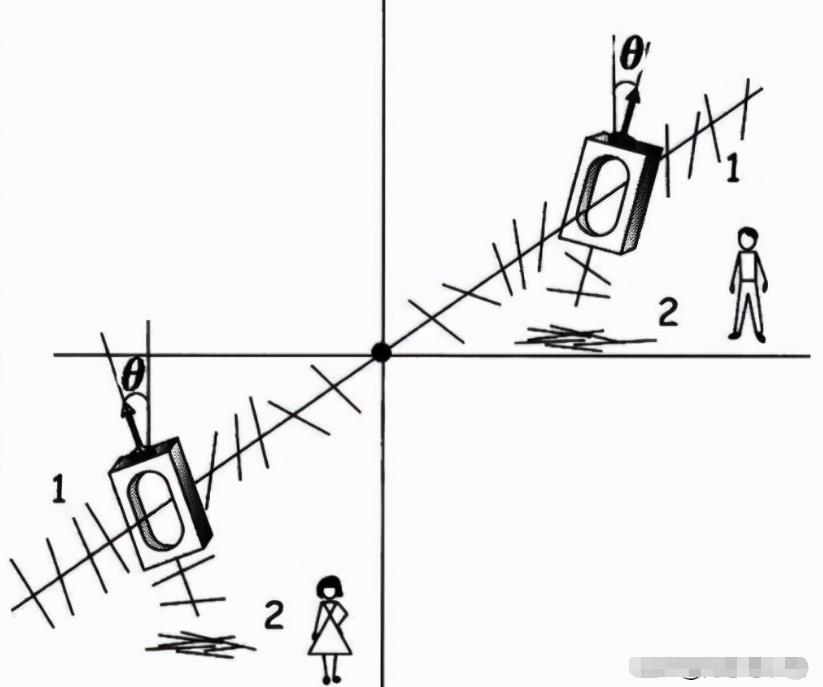
来自《量子之谜》(Quantum enigma)
之所以,两边需要向不同的方向旋转,是因为如果同向,就相当于相对没有旋转,这和两边都不旋转的结果是一样的,即两边的记录保持一致。
我们仍然设置,检偏器θ = 30度,即:女孩左旋30度,男孩右旋30度,并想象一下:此时,错配率会是多少呢?
显然,左边旋转会带来25%的「记录1对记录2」,右边旋转会带来25%的「记录1对记录2」,合起来就是「25% + 25% = 50%」的「记录1对记录2」。
但我们需要考虑到,25%是「记录1变成记录2」的概率,又由于两边都会有这个概率,于是就会出现两边同时发生「记录1变成记录2」的可能,这会产生「记录2对记录2」的匹配结果,而如果两边25%全部以「记录2对记录2」的形式匹配上(比如全是垂直偏振),即:错配率最小是0%。
因此,理论上我们可以认为,错配率在0%到50%之间,最大值就是50%——而这个理论上错配率必定小于50%的要求,就是贝尔不等式成立的实验要求。
然而,实验的统计结果却是:75%大于50%,这怎么可能呢?
结果说明
理论上,两边同时反向旋转θ角度的错配率,一定小于等于,两次单边旋转θ角度的错配率之和。
用公式表达,即:左旋θ角度且右旋θ角度 ≤ 左旋θ角度 + 右旋θ角度,而这个不等式就是——贝尔不等式。
接着我们考虑,左旋θ角度且右旋θ角度——两边检偏器的角度差(即夹角)就是2θ,又由于空间性质在所有方向上都是相同的,所以这种设置就等价于——保持角度差2θ,并将一边调整至不旋转,即:一边不旋转、一边旋转2θ角度。
因此,贝尔不等式就转换成了:单边旋转2θ角度 ≤ 左旋θ角度 + 右旋θ角度。
然后,我们将量子力学的公式带入后,得到不等式:sin^2(2θ) ≤ sin^2(θ) + sin^2(θ) 。
最后,我们将实验设置,检偏器θ = 30度带入不等式:sin^2(60°) ≤ sin^2(30°) + sin^2(30°),即:0.75 ≤ 0.5。
显然,75%大于50%就是实验结果,且表明贝尔不等式不成立。
不成立的意义
第一,孪生光子的偏振是“观测确定”,而不是“出生确定”。
因为观测确定意味着,孪生光子的偏振,直到来到检偏器的时候才随机出一个方向,并且两边的孪生光子不是各自随机,而是协调随机一致。
也只有这样,孪生光子才能通过瞬间协调,在“发现”两边检偏器反向旋转的时候,当即随机出一个更高的错配率,使得最终的结果符合量子力学的预测值。
相反,如果是出生确定,即孪生光子没有针对“反向旋转”,进行临时的“协调随机”,那么最终的错配率就不会违反,贝尔不等式要求的最大值。
第二,隐变量与定域性,不能同时存在,或都不存在。
孪生光子的偏振,如果是出生确定——就是隐变量存在且定域性存在,即:孪生光子在出生时刻,带有某个隐变量,其偏振方向由这个隐变量确定,而不是观测确定,并且孪生光子之间无需进行瞬间协调(因为由隐变量保证一致)。
孪生光子之间是否有非定域性,只需要在上述实验的时候,将两边检偏器相距很远,光速传递信息都无法瞬间协调,即可验证这点——结论是有瞬间协调。
与贝尔不等式不成立,等价的说法还有:
实在性与定域性,不能同时存在,或都不存在。
定域性隐变量是不存在的。
定域实在性是不存在的。
第三,孪生光子的瞬间协调(即非定域性),并不能传递信息,所以它并没有违反相对论与因果关系。
可见,定域性维护了因果,但非定域性却不一定违反因果(如量子纠缠)。然而,实在性与非定域性同时存在,会发生超光速传递信息,并破坏因果,这是不符合观测结果的。
最终,我们可能需要——放弃隐变量与实在性,在不违反因果的情况下,放弃定域性。而放弃定域性,其实就是放弃独立性,那么在因果之外(即光锥之外),只有一个整体。
实验:单电子双缝干涉
一个一个发射电子,通过双缝挡板,击中挡板后的侦测屏,每次等到侦测屏显示电子击中后,才发射第二个电子。
反复发射多个电子,最终在侦测屏上,记录电子所形成的图案,显示出了干涉条纹。如果封闭一个缝隙,变成单缝隙,侦测屏则没有干涉条纹出现。
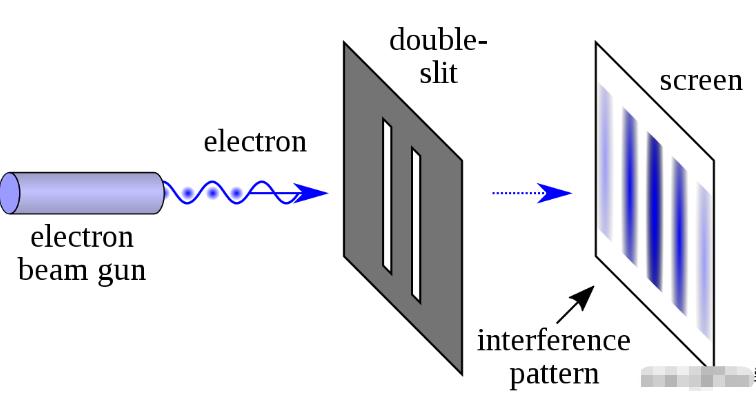
来自维基百科(Double slit experiment)
这个实验,与光的干涉实验完全不同,因为光的干涉是光通过双缝,形成两组光波,最后产生干涉条纹。而这里是单个电子通过双缝,最终也形成了干涉条纹,前者是群体,后者是个体。
这里有几点需要说明的是:
第一,多个电子在侦测屏上,形成的干涉条纹,是符合波函数的概率分布预测的。
第二,一个电子在侦测屏上,只能是一个点,而不是干涉条纹,需要多次发射电子,才能形成概率分布图案——产生干涉条纹,此时单个电子在群体事件中,显示出了统计属性。
第三,干涉条纹意味着,单电子通过双缝时,产生了波的干涉效应,相当于电子同时通过双缝,产生了两个波源,然后自己和自己干涉。
第四,如果单电子每次只是随机的通过一条缝隙,就不会在双缝之后自己和自己干涉,那么最终的图案就不会出现干涉条纹,而只会是两条明亮的条纹。
这个实验说明了,单电子具有波动性:就是单个电子在空间中的位置是不确定的——呈现一种概率分布,这种位置分布的概率能够叠加,形成自我干涉效应——就是增加某些位置出现的概率,减少某些位置出现的概率。
最终,电子击中侦测屏,它的波动性转变为粒子性,也就是概率给出结果,即位置确定。而实验结果形成干涉图案,就体现出了一个电子的波动性与自我干涉叠加。
因为实际上,在干涉条纹中,所有点都对应着电子能够随机到的位置,而只有电子呈现波动性,并且自己和自己干涉,才会产生那些明暗点的位置概率,从而形成明暗条纹。否则,就只会有两条亮色条纹的位置概率,而不会有暗色条纹的位置概率。
实验:观察者双缝干涉
与单电子双缝干涉实验一样,只不过,在双缝挡板前进行观测,以确定单电子如何穿过双缝。结果是,观测到每个电子随机穿过了一条缝隙,侦测屏最终的干涉条纹消失,只有两条明亮的条纹。但去除观测手段,干涉条纹就会再次出现。
这个实验正是说明了,波粒二象性的互补原理,其体现出了一种“观察者效应”,即:
如果观测,粒子给你展现的就是粒子性,并且波动性就退化了。
如果不观测,那么粒子的波动性就又会出现,并且粒子性就退化了。
实验:光子延迟选择
一个光子,射入一个分束器(Beam Splitter),那么就有一半的概率穿过,一半的概率被反射,这是一个量子随机的过程。
分束器——是可将一束光分成两束光,或多束光的光学装置,它是大多数干涉仪的关键部分,通常是由金属膜或介质膜构成。
而分束器有个特性,如果光被镀膜面反射(下图右上BS2下方蓝色线),光的相位会增加(相移);如果光被玻璃面反射(下图右上BS2上方黑色线),光则不会增加相位;如果光被透射,无论哪一面都不会增加相位。
相位——就是一个波,其循环中的位置,如:波峰、波谷、或是峰谷之间某个点的标度。
这个特定的意义在于,通过调节分束器的角度,就可以调节分离后两束光的相位差,从而让它们再次相遇时,产生干涉效应。
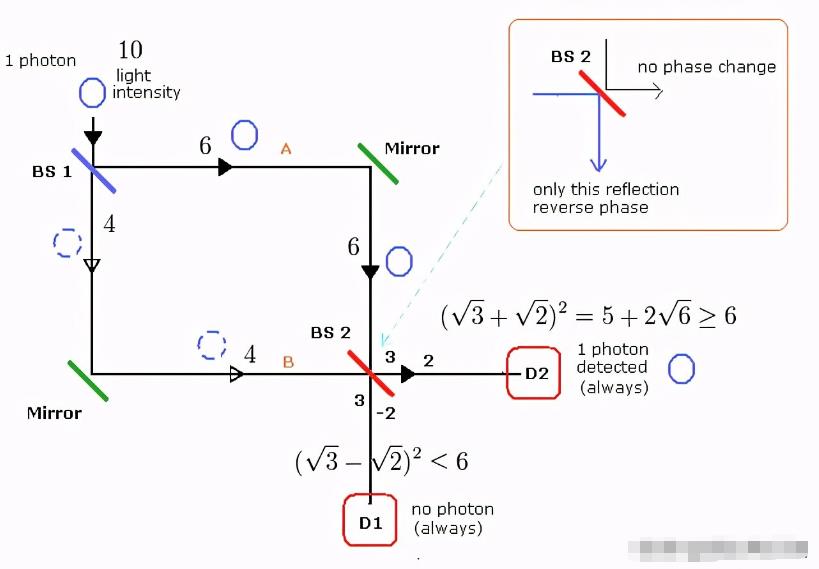
来自必应搜图
第一种情况,在分束器(BS1)两边,放置侦测屏(D1D2,此时没有BS2),就可以检测光子是穿过分束器,还是被分束器反射。结果显示,每个光子,只会随机让一个侦测屏产生亮点,多次之后依旧是亮点。这说明了,光子每次只会穿过或被反射。
第二种情况,利用两个反射镜(Mirror),将可能穿过分束器(BS1),或是被分束器反射的光子,继续导入第二个分束器(BS2)的两面。也就是说,如果光子穿过第一个分束器,则会进入第二分束器的一面;如果光子被第一个分束器反射,则会进入第二个分束器的另一面。
要知道,第二个分束器依然有一半的概率,让光子穿过或反射。那么接下来,在第二个分束器的两边,放置侦测屏(D1D2),以检测穿过或被反射的光子。
结果显示,每次发射一个光子,经过多次,在其中一个侦测屏上,出现出了干涉条纹。
这说明了,一个光子进入第一个分束器,同时穿过和被反射,然后按照两条路径运行的光子,同时进入第二个分束器的两面,又继续同时穿过和被反射。
那么,在第二个分束器的两面,都会有穿过和反射的光子。通过调整光子的相位,就可以让光子自己和自己,在一面相互抵消,在另一面相互干涉,从而在一个侦测屏上,产生干涉条纹。
第三种情况,在光子经过第一个分束器的过程中(BS1),并没有第二个分束器(BS2),这相当于第一个情况,光子会穿过或被反射。然后在光子完成第一个分束器的量子随机后(穿过或被反射),再“延迟”加入第二个分束器(BS2)。
结果显示,与第二种情况一致,光子会同时穿过和被反射。
这说明了,我们“延迟”加入第二个分束器(BS2)的行为,让光子已经确定第一种情况的选择后,神奇地切换到了第二种情况。这样,我们的延迟选择,就决定了已经完成的选择。
对于这个实验,惠勒后来引用玻尔的话说:
“任何一种基本量子现象,只在其被记录之后才是一种现象,我们是在光子上路之前,还是途中来做出决定,这在量子实验中是没有区别的。光子在通过第一块透镜,到我们插入第二块透镜这之间,它到底在哪里,是个什么,是一个无意义的问题,我们没有权利去谈论它,因为它不是一个客观实在!”
实验:量子擦除
这个量子擦除实验(Quantum Eraser Experiment)有些复杂,但也被成功验证。

来自必应搜图
第一步,我们创造出一对纠缠态的光子,间隔发射,通过双缝板——上面有缝A和缝B,并且这一对光子,在通过双缝的时候不分离。但我们不知道这一对光子,是通过A、还是B、还是同时通过AB。
第二步,这一对光子,通过双缝后,如果在A处会被分离为纠缠态的两个光子——A1A2,如果在B处会被分离为纠缠态的两个光子——B1B2,其中A1和B1将会进入透镜,被集中到D0侦测屏,最终显示出干涉条纹。
此时,D0上的光子,无法区分哪些是A1,哪些是B1,这就意味着,不知道这些光子来自哪个缝隙——A或B。
显然,是纠缠态的一对光子同时进入了AB,然后同时在A分离出A1,在B分离出B1,并且A1和B1在透镜之后产生干涉,才能在D0显示出干涉条纹。
第三步,A2和B2将会进入偏光镜,分别走向不同的方向。并且去向的地方,均在远离D0的位置,这说明了在A2和B2仍在运动的过程中,D0已经检测到光子。
第四步,A2进入分束器,有50%的概率进入侦测屏D4,另外50%的概率进入分束器,之后又有50%的概率(50%中的50%就是25%的概率)进入侦测屏D1,和50%的概率(50%中的50%就是25%的概率)进入侦测屏D2。
同理,B2进入分束器,有50%的概率进入侦测屏D3,另外50%的概率进入分束器,之后又有50%的概率(50%中的50%就是25%的概率)进入侦测屏D1,和50%的概率(50%中的50%就是25%的概率)进入侦测屏D2。
总结起来就是:
A2有50%概率进入D4,25%的概率进入D1,25%的概率进入D2;
B2有50%概率进入D3,25%的概率进入D1,25%的概率进入D2;
可见,D1D2无法区分A2B2。
第五步,D1和D2侦测屏,都没有反应。那么,这个时候如果D4有反应,说明是A2(状态坍缩),与之纠缠态的A1——会在D0产生反应;如果D3有反应,说明是B2(状态坍缩),与之纠缠态的B1——会在D0产生反应。
于是,通过D4和D3的反应(不会同时反应),我们就知道了在D0处的是A1还是B1,然而此时,D0处的干涉条纹就消失了。
显然,这是因为我们确定了这一对纠缠光子,通过AB缝的准确路径,于是这一对光子的状态坍缩,展现出了粒子性,只能在AB中选择一个通过。
第六步,D1和D2侦测屏,其中一个有反应。此时,A2和B2都有概率形成这个结果,那么我们依旧无法确认,A1和B1谁在D0处产生了反应,即意味着,A1和B1都在D0处,产生干涉,自然干涉条纹就再次出现在了D0。
至此,整个实验完成,有两点值得说明:
第一,D1和D2侦测屏有没有反应是概率,从结果来看:在D1或D2有反应的时候,D0有干涉条纹——这相当于擦除了路径信息;在D1和D2没有反应的时候,D3或D4会有反应——这相当于拥有了路径信息,此时D0干涉条纹消失。
第二,从第三步可知,光子抵达D1234的距离,要长于D0。所以,D1234有没有反应的时候,D0早已出现过了反应——形成条纹,但D0处的条纹是否干涉,依然受控于,后发生的D1234的反应。
这个实验的重点,在于揭示了:粒子状态的坍缩,不在于观察者,或是什么样的观察者——包括观测技术设备、有无智能和意识等等——而是在于信息路径的构建。
实验现象的各种解释
前面的实验,已经毫无悬念地证明了微观粒子的波粒二象性——与宏观现象完全不同,让人感觉匪夷所思,并且十分难以理解。
但实验结果是不容置疑的,于是人们纷纷针对实验结果,开始了各种虚幻的自我解读,以下列举出一些具有代表性的解释:
没有粒子只有波
我们处在无处不在的,就像是汤一样的量子场之中,这些汤(能量场)就像波一样运动。只有在我们观测时候,粒子才会从汤中涌现出来——就像被我们的观测行为给召唤了出来一样。
没有波只有粒子
粒子的运动速度超级快,而我们的观测(曝光)速度又太慢。所以,当我们进行一次观察的时候,所捕获到的图像,其实是粒子快速去到不同地方的样子,而在我们看来就是粒子同时出现在多个地方的样子,所以我们会说粒子有波一样的状态。
没有波也没有粒子
粒子,只是我们根据观测的属性,抽象成了一个宏观唯象的模型。然而,在不同的情况下,根据观测属性,又符合宏观波的唯象模型,所有才会有波粒二象性,这种在宏观下矛盾的状态描述。其实,这些微观物质的本质,是非波非粒的,具体是什么,我们也不知道,目前没有具体的图像。
有波有粒子
微观的物质,在没有观测的时候,是“云”或“雾”的形态,以波的形式运动,只有在观测的时候,才会汇聚到“一点”成为一个粒子。为什么会这样?这是因为“云”或“雾”的能量状态,因为观测受到的干扰,能量丢失变小只能形成一个点,就是粒子。
高维度宇宙
微观物质,是高维度宇宙的投影,它们的行为状态变化莫测,是因为我们只能看到了,这些高纬度投影的片段,所形成的难以理解的运动轨迹和特征形态。
多重宇宙
微观粒子波的特性,是来自于,无数个平行宇宙的粒子,同时叠加的影像。然而,一旦观测,平行时空就会分离,单个粒子就会出现在特定唯一的当前时空。
谁敢保证——平行宇宙以后就不是现实呢?以前不是就出现过地球中心论与太阳中心论吗?历史不总是在重复,并且还押韵吗?
路径积分表述
在纯粹数学上,路径积分表述,不采用粒子的单独唯一运动轨道,取而代之的是所有可能轨道的总和。使用泛函积分,就可以计算出所有可能轨道的总和。也就是说,微观粒子从一个地方,去到一个地方,会选择可能的所有路径(包括同时穿过双缝),而观测会让观测位置与粒子之间,形成唯一的路径,从而选择消失。
实验质疑
在这些实验中,是如何发射一个电子或是一个光子的,存在一个电子或是一个光子吗?首先假定,有电子和光子,然后再在实验中发现了这些粒子的波动性,这不是一种矛盾吗?
哥本哈根诠释
微观粒子在测量之前,其空间位置是不确定的,所以试图讨论,测量之前的粒子轨迹和路径是没有意义的。所有的不解和困惑,都显然来自于,讨论了不应该讨论的主题。
结语
事实上,一个成功的解释,是可以预测未来所有的情况的,如果可以做到,那么这个解释基本就是一种正确的视角。
事实上,“波函数现实”则完美地以概率的形式,预测了微观粒子的波动性与粒子性,只不过人们还迫切想要知道的是,这些概率到底是如何形成的——也就是在观测之前都发生了什么。
弦理论专家——布赖恩·格林(Brian Greene),在《宇宙的琴弦》中说道:
“每个人都知道怎么用量子理论的方程来做精确的预言,但是,关于概率的意义,关于粒子如何「选择」它的未来,还没有一致的认识;甚至,我们还不知道粒子是不是真的选择了一个未来;也许,它会像树枝那样分开,向着不断膨胀着的平行宇宙展开它各个可能的未来。”
追根究底,其实是人们,并不满足于概率与不确定性——这个答案,因为在我们根深蒂固的意识里——一切都是确定的,这是源自于我们本能感知的结论。
而更底层原因可能在于,连接微观到宏观的是概率,但我们处在宏观,理论上概率已经形成了确定的结果,所以我们只能看到确定性,而看不到不确定性,并且我们还试图用宏观的感知,去解读微观的一切。
或许,束缚我们的就是宏观,而无法抵达微观的路径——就是信息。
原文链接:http://www.toutiao.com/a6949458984453653025
本站文章部分来自于互联网,已注明出处。 未注明原文出处皆为原创文章,转载同样请注明出处并添加链接。
猜你喜欢
发表评论
电子邮件地址不会被公开。 必填项已用*标注