波粒二象性?泡利不相容原理?哪个才是最重要的量子规则?
地球上的所有东西都是由原子以及他们构建块组成的。如果没有这一条规则,它们将永远不会构成什么有趣的东西。
看一下你周围的一切事物。如果你要研究任何物质的组成形式是什么,你可以将它不断地细分为越来越小的块。所有活着的生物都由一个个的细胞组成,这些细胞则是一个个复杂的分子集合,而分子则是由一个个原子组合在一起。原子也可以被继续细分,分为原子核和电子。这些就是地球上所有物质的组成部分,就此而言,我们所有已知的宇宙中的正常物质也是由此组成的。
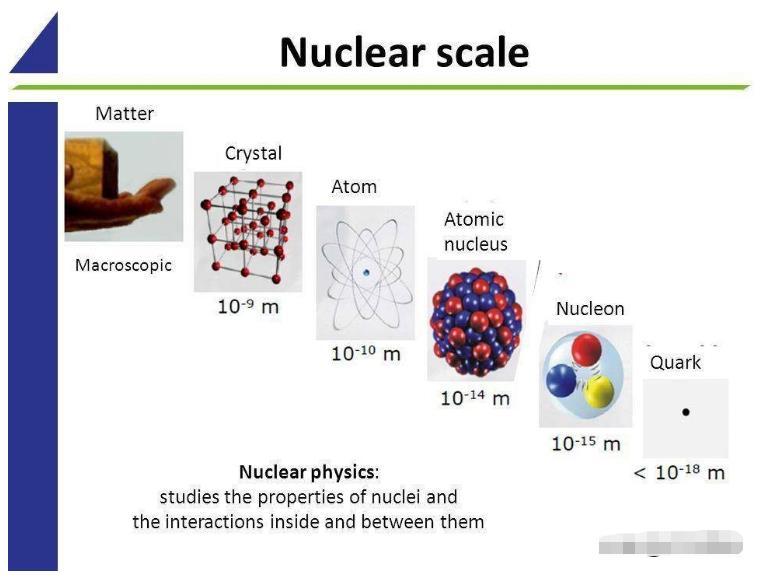
图解:从宏观尺度到亚原子尺度,基本粒子的尺寸在决定复合材料结构尺寸中只起到很小的作用。这些构造块是否是真正的基本粒子和/或点状粒子尚不清楚,但我们确实了解宇宙从大的宇宙尺度到小的亚原子尺度。(MAGDALENA KOWALSKA/CERN/ISOLDE团队)
你可能想知道这一切时如何发生的。由原子核和电子组成的,不到100种的,原子是如何能构建出数不尽种类的分子、物质、生物以及我们认知中的一切。我们将这个答案归功于一个被低估的量子规则:泡利不相容原理(the Pauli Exclusion Principle)。

图解:原子轨道处于基态(左上角),下一个能量最低的状态随着你向右和向下移动出现。这些基本的配置决定了这些原子如何表现和原子间作用力。(维基百科关于原子轨迹的页面)
当我们中的大部分人在思考量子力学时,我们在最小尺度上思考宇宙中那些怪诞和违背直觉的特征。我们考虑海森堡不确定性,以及不可能同时知道超出有限的相互精度的成对物理属性(比如位置和动量、能量和时间、或两个垂直方向上的角动量)这一事实。
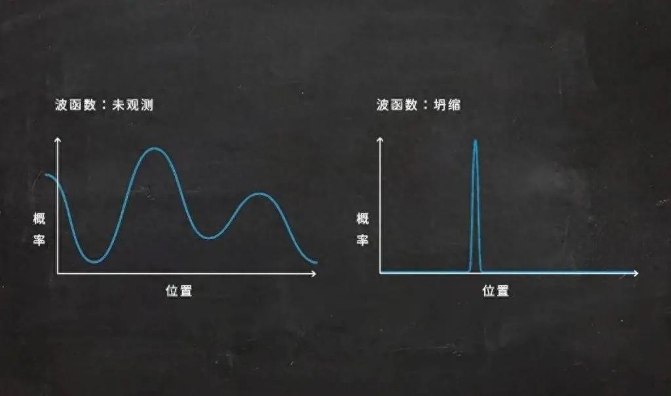
我们考虑物质的波粒二象性,以及对单个粒子(如电子或光子)好像会干扰自身的行为研究。我们常常提及薛定谔的猫,以及量子领域可以同时存在多种可能结果的组合,只有当我们进行关键的、决定性的测量时,多种结果才会坍塌到一种特定结果上。
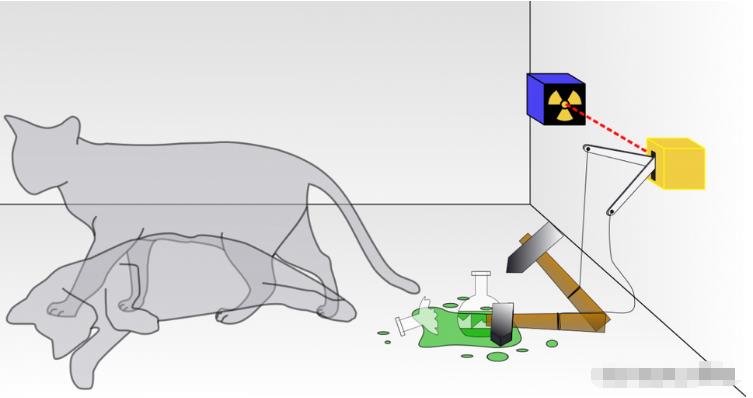
图解:薛定谔的猫是一个理想实验,旨在说明量子力学中怪诞和违背直觉的本质。量子领域可以处于多个状态的叠加,直到进行关键的观测或测量,此时只有一个可测量的结果。
我们大部分人几乎没有再去思考过泡利不相容原理,该原则简单说明了在同一系统中没有两个相同的费米子可以占据相同的量子态。
很重要,对吧?
事实上,这不仅仅是重要,这几乎是其中最重要的一点。当波尔第一次推出他的原子模型时,它很简单但是及其有效。通过将电子视为围绕原子核运动的行星状实体,但是仅在明确的能量水平上由直接的数学规则控制,它的模型重现了粗糙的物质结构。当点在在能量等级之间转换时,它们发射或吸收光子,这反过来描绘了每个单独元素的光谱。
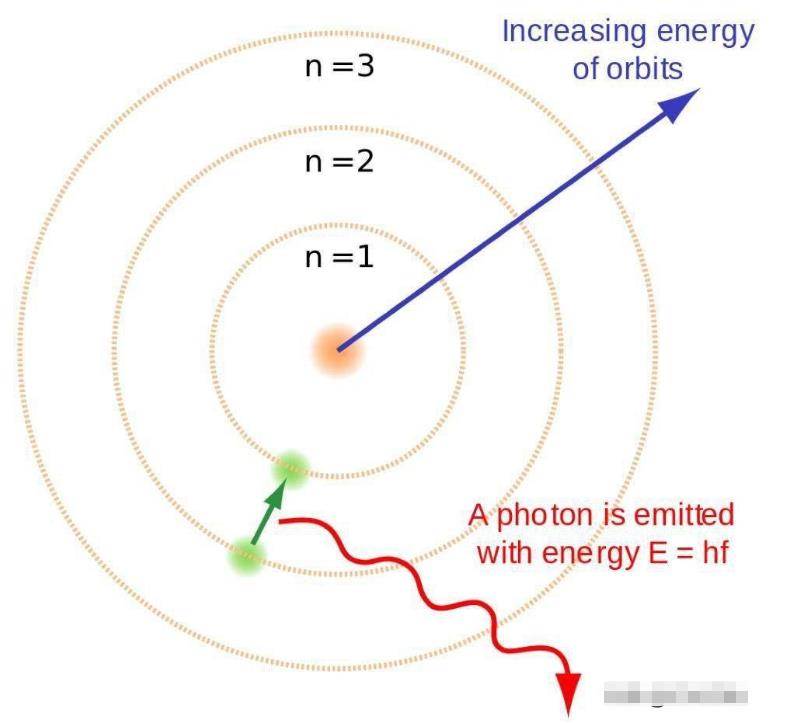
图解:当自由电子与氢原子核重新结合时,电子的能量等级会急速下降,发射光子。为了追求稳定,在早期宇宙中形成的中性原子,它们必须达到基态而不产生潜在的电离紫外光子。波尔德原子模型提供了一个粗糙的能量等级结构,但是这还不足以解释几十年前见到过的东西。(BRIGHTERORANGE & ENOCH LAU/WIKIMDIA COMMONS)
如果不是泡利不相容原理,我们宇宙中的物质会以一种截然不同的形式表现出来。你看,电子就是一种费米子的例子。每个电子基本上与宇宙中的每个其他原子相同,具有相同的电荷、质量、轻子数、轻子族数和内在角动量(或自旋)。
如果没有泡利不相容原理,那么可以填充原子基态(最低能量)的电子数量就没有限制。随着时间的推移,在足够低的温度下,宇宙中每一个原子最终都会沉入这个状态。最低能量轨道—每个原子中的1s轨道—将是唯一包含电子的轨道,同样它将包含每个原子中的固有电子。

图解:这位艺术家的插图展示了一个绕原子核运动的电子,其中电子是一个基础粒子,但是原子核可以背继续分解成更小,更基础的成分。(NICOLLE RAGER FULLER, NSF)
当然,这并不是我们宇宙的运行原理,而且这是一件非常好的事。泡利不相容原理正是通过这个简单的原理来预防这种情况的发生:你不能将使个相同的费米子处于同一量子状态。
当然,第一个电子可以滑入最低能量状态:1s轨道。然而,如果你尝试将第二个电子放在那里,它不能具有与先前电子相同的量子数。电子,除了那些它们本身就具有的量子性质(如质量、电荷量、轻子数等)。当它们与原子核结合时,那还将包括能级、角动量、磁量子数和自旋量子数。
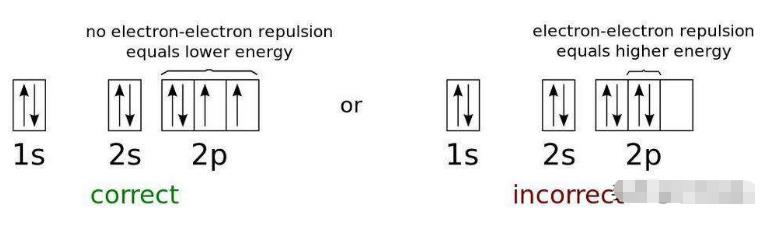
图解:电子能量表示中性氧原子的最低可能能量构型。因为电子是费米子而不是玻色子,即使是在任何低温情况下,它们也不能全存在于基态(1s)中。这是阻止任何两个费米子占据相量子态,并且大多数物体抵抗重力坍塌的物理学。(CK-12 FOUNDATION AND ADRIGNOLA OF WIKIMEDIA COMMONS)
原子核中最低能量状态的下的电子占据了最低能量级(n=1),而且将不具有角动量(l=0),因此磁动量同样也是0。然而,电子的旋转缺提供了第二种可能性。每个电子的自旋都是1/2,原子中能量最低状态(1s)也是如此。
当你加入第二个电子,它同样可以自旋,但是是往一个相反的方向,有效旋转 —1/2 。通过这种方法,你可以将两个电子装入1s轨道。在这之后,第一能级就满了,然后你必须前往下一能级(n=2)去添加第三个电子。这个2s轨道(这里与上一能级一样 l = 0)可以容纳另外的两个电子,然后你必须前往2p轨道(l=1),这里可以容纳三个磁量子数:—1、0或是+1,而且每个都可以保持电子自旋为 +1/2 或 —1/2 。
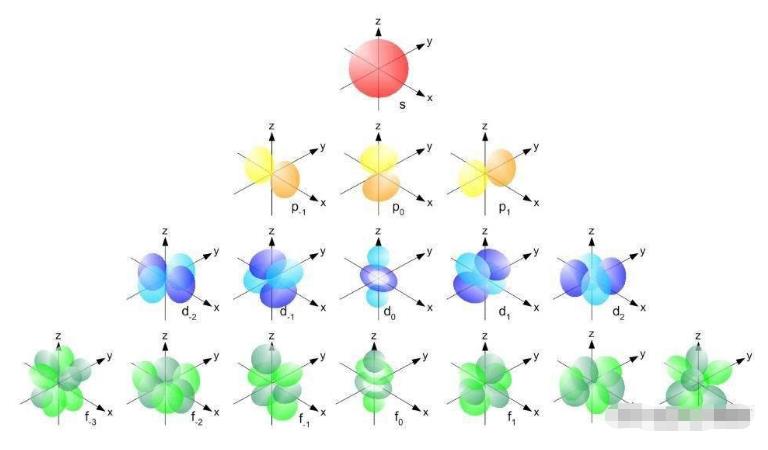
图解:每一个s轨道(红色),每个p轨道(黄色),每个d轨道(蓝色)和每个f轨道(绿色)每个都只可以容纳两个电子:一个向上旋转,一个向下旋转。(LIBRETEXTS LIBRARY / NSF / UC DAVIS)
泡利不相容原理—以及我们宇宙中拥有的量子数的事实—赋予了每个原子它们自己独特的结构。随着我们加入更多数量的电子到原子中,我们不得不前往更高的能级、更大的角动量和更加复杂的轨道为每一个电子寻找位置。这些能级的工作方式如下所示:
最低的能量级(n=1)只有s轨道,它没有角动量(l=0)并且只能容纳两个电子(自转为 +1/2 和 —1/2)
第二个能量级(n=2)包含s轨道和p轨道,它可以拥有0(l=0)或1(l=1)的角动量,这也意味着你可以在2s轨道(在2s轨道你可以放置自转为 +1/2 和 —1/2的电子)放置两个电子,并且在2p轨道(磁量子数 —1,0和+1,每个都容纳着自旋+1/2 和 —1/2的电子)可以容纳6个电子。
第三个能量级(n=3)有s、p和d轨道,d轨道的角动量为2(l=2),因此磁量子数可以达到五个(—2,—1,0,+1,+2),所以总共可以容纳10个电子,除此之外还有3s轨道(容纳两个电子)和3p轨道(容纳六个电子)。
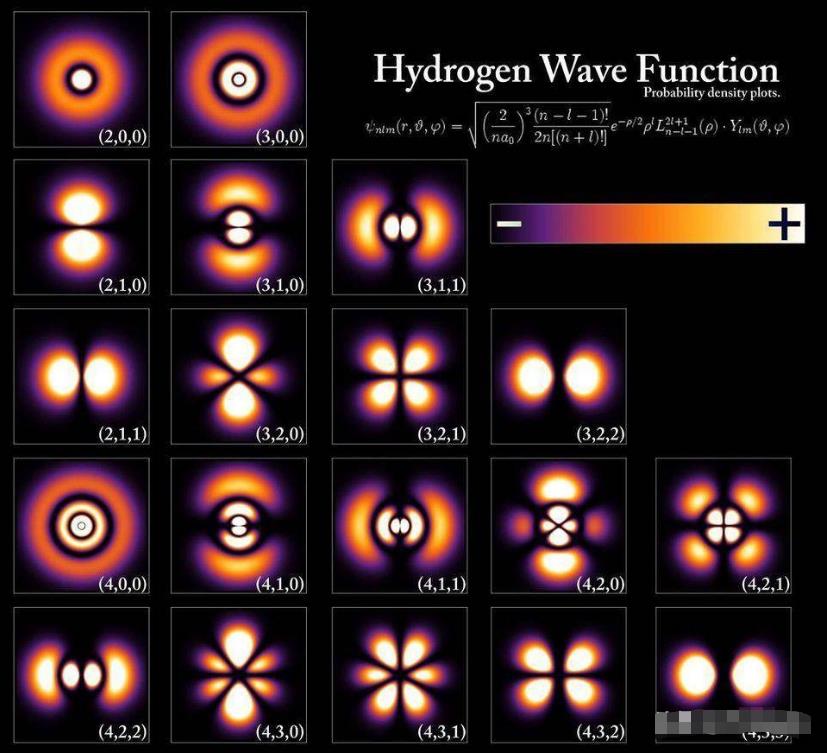
图解:能量级和电子波函数对应氢原子内的不同状态,尽管所有的原子结构都极其的相似。能量级由普朗克常数倍数量化,但是轨道内原子的大小由基态能量和电子质量决定。额外的影响可能是非常微小的,但是可以通过可以衡量的、可以量化的方式来概念能量级。(POORLENO OF WIKIMEDIA COMMONS)
在这个关键的量子规则下,元素周期表上的每一个原子都将具有与其他原子不一样的结构。因为最外壳中的电子特性决定了它的物理和化学特性,所以每一个原子都有自己形成自己独特的原子、离子和分子键。
无论两种元素多么相似,他们在形成的结构方面都是不同的。这也是我们可以用几种简单的原料来构建复杂结构的根本。我们添加的每一个新电子都必须具备与之前电子不同的量子数,这将改变原子与其他所有物质作用的方式。

图解:原子连接成分子的方式,包括有机分子和生物过程,都是因为有泡利不相容原理管理电子才成为可能。(JENNY MOTTAR)
最终的结果是,每个单独的原子为原子结合形成化学或生物化合物提供了无数种可能性。原子的结合方式是没有限制的。当然一些结构需要耗费更多的能量,自然界中存在各种各样的能量条件,为这些化合物的形成铺平了道路,即使是最聪明的人类也难以想到。
我们可以通过组合原子来形成许多奇妙的化合物,原子能表现出这种行为的唯一原因就是,我们不能将任意数量的电子放入同一量子态。电子即是费米子,而泡利这一未被完全理解的量子规则阻止任何两个相同的费米子拥有同等数量的量子数。
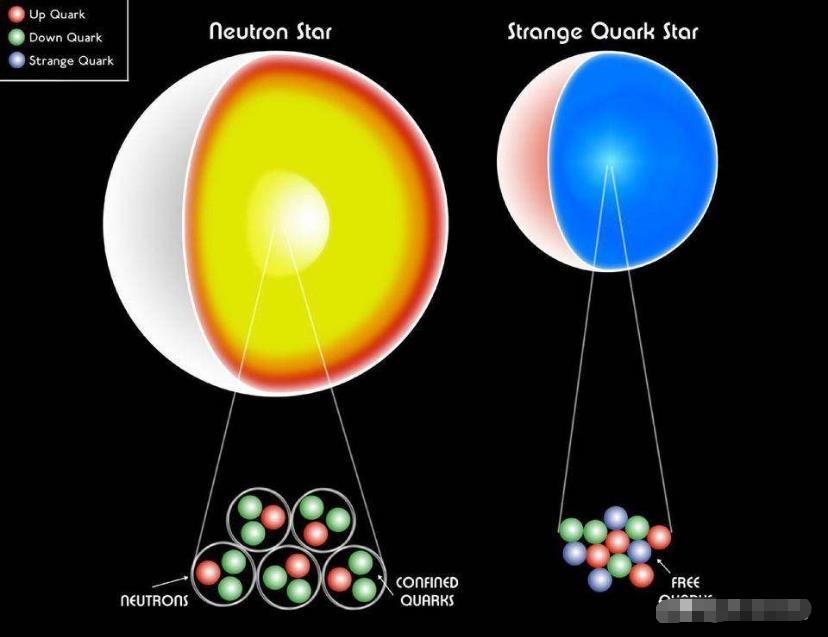
图解:白矮星,中子星,甚至最奇怪的夸克星都是由费米子组成。泡利简并压力帮助所有恒星残余物抵抗重力坍塌,防止其形成黑洞。 (CXC / M.WEISS)
如果我们没有泡利不相容原理来阻止多个费米子获得相同的量子态,我们的宇宙将会非常不同。几乎每一个原子都会具有和氢原子一样的性质,且能组合成的结构也是及其简单的。由泡利不相容原理提供的简并压力才存在的白矮星和中子星也将会坍塌成黑洞。更恐怖的是,所有的碳基化合物— 所有生命的基础— 将不会存在。
当我们想到控制现实的量子规则时,通常泡利不相容原理不是第一个,但它应该是。没有量子不确定性或波粒二象性,我们的宇宙将会变的不同,但是它仍将存在。然而,如果没有泡利不相容原理,氢之间的分子键及那些类似的分子
原文链接:https://www.toutiao.com/article/6799430828737692168
本站文章部分来自于互联网,已注明出处。 未注明原文出处皆为原创文章,转载同样请注明出处并添加链接。
猜你喜欢
发表评论
电子邮件地址不会被公开。 必填项已用*标注